funkcje Karolina: Czesc, może ktoś pomóc z tymi zadaniami?\ Wylicz wartość: a)arcsin(sin(−4)) b)arccos(cos(−9)) c)arctan(tan3)

	3
d)sin(arccos(−		))
	4

	4
e)tan(arccos(−		))
	5

	1		3
f)sin(arcsin(		+ arcsin		)
	3		4

	1		3
g)sin(arcsin(−		) − arccos		)
	√5		√15

Bo przepadły mi ćwiczenia z tego i kazano nam samemu przerobić ten materiał, a nie mogę znaleźć nigdzie tego na necie, jak ktoś ma jakieś przydatne materiały do tego, to z góry dzięki

Blee: a na wykładach byłaś

Blee: https://www.wolframalpha.com/input/?i=arcsin(sin(-4))

Blee: arcusy to funkcje odwrotne do funkcji trygonometrycznych, więc arcsin(sin(x)) = x +/− kπ (jeżeli x jest poza − π/2 ; π/2) analogicznie pozostałe funkcje

Blee: arccos(−3/4) = arcsin(√7/4) (ponieważ: 4² = (−3)² + (√7)²) ... natomiast znak wynika z wykresu funkcji cyklometrycznych więc sin(arccos(−3/4)) = sin(arcsin(√7/4) = ... patrz wcześniejszy mój wpis

Karolina: No na wykładach podano nam tylko arcsin(x)+arccos x= pi/2 oraz arctan(x)+arccot x=pi/2

Karolina: Czyli arccos(x)=arcsin(y) , gdy x²+y²=1?

Blee: sprawdź czy (f) NA PEWNO tak wygląda

Blee: (e) −−− arccos(−4/5) = x oznacza, że:

	√52 − 42
x = arcsin(		= arcsin(3/5)
	5

więc x = arctg(−3/4) więc tg(arccos(−4/5)) = tg(arctg(−3/4)) = −3/4

Karolina: W f nawiasy pogubiłam...

	1		3
sin(arcsin(		)+arcsin(		))
	3		4

Blee: (f) masz tutaj obliczyć: sin(α + β) = sinα*cosβ + cosα*sinβ = sin(arcsin(1/3))*cos(arccos(3/4)) + cos(arcsin(1/3))*sin(arcsin(3/4)) jak sobie poradzić z sin(arcsin(x)) już wiesz, jak sobie poradzić z cos(arcsin(x)) też już wiesz (pokazałem w poprzednich przykładach) więc powinnaś sobie poradzić analogicznie robisz ostatni podpunkt

Blee: miało być: sin(α + β) = sinα*cosβ + cosα*sinβ = sin(arcsin(1/3))*cos(arcsin(3/4)) + cos(arcsin(1/3))*sin(arcsin(3/4))

Karolina: Dzięki wielkie, zaraz spróbuję wyliczyć

Karolina: "arcsin(sin(x)) = x +/− kπ (jeżeli x jest poza − π/2 ; π/2) analogicznie pozostałe funkcje" Czy możesz wyjaśnić bliżej, kiedy +, kiedy − oraz wartość k?

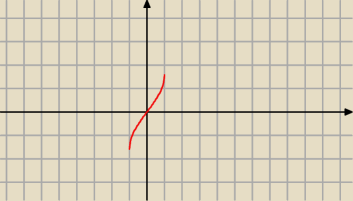
Blee: funkcja f(x) = arcsin(x) ma dziedzinę <−π/2 ; π/2> zauważ, że sin(−4) = −sin(4) = − ( −sin(4−π)) = sin(4−π) <−−− wynika to ze wzorów redukcyjnych: https://matematykaszkolna.pl/strona/430.html powyższe przekształcenia są konieczne ze względu na dziedzinę i zbiór wartości funkcji cyklometrycznej i właśnie dlatego arcsin(sin(−4) = 4 − π (która to liczba należy do <−1;1>) a nie −4. I z pewnością to będzie jedna z rzeczy na którą będą chcieli 'złapać' studentów ćwiczeniowcy.

Karolina: Dzięki Wszystko jest teraz zrozumiałe

Karolina: Większość zadań udało mi się poprawnie wykonać, ale czy mógłbyś jeszcze proszę wyjaśnić arccos(−3/4) = arcsin(√7/4) (ponieważ: 42 = (−3)2 + (√7)2) ... natomiast znak wynika z wykresu funkcji cyklometrycznych Jak te wykresy analizować, aby to z nich wynikało? Już ostatnia rzecz, obiecuję, dziękuję za cierpliwość

	3
Ogólnie ogarnąłam (arccos(−		)=(π−arcsin{√7}{4}) i potem już jadę ze wzoru na sumę
	4

sin(α+β), tylko widzę, że ty to szybciej zrobiłeś, a jak wiadomo czas na kolokwium najważniejszy