planimetria planimetria: Punkty A=(7,−4) i C=(6,5) są przeciwległymi wierzchołkami trapezu ABCD a prosta o równaniu y=3 jest jego osia symetrii.Oblicz współrzędne punktów B i D (1), współrzędne środka O okręgu opisanego na tym trapezie (2) i długość jego promienia R (3). (1) zrobione: wyszło mi, że B=(7,10) i D=(6,1) (2) wyznaczyłam długości |AS|, |CS|, |DS|, |BS| − jeśli przyrównuję |AS|=|BS| wychodzi mi wynik poprawny; jeśli |CS|=|DS| − wychodzą mi pierdoły − skąd ta różnica? (3) jeśli zrobię (2) to nie będzie żadnego problemu, póki co nie mam Jeśli mogłabym prosić to byłabym bardzo wdzięczna za pomoc w (2)

Blee: (1) okey (2) po pierwsze −−− środek okręgu na pewno leży na prostej y=3 (oś symetrii). Jak już to powinno się porównywać |AS| i |CS| lub |DS| (każdy punkt na osi symetrii będzie spełniał równość |AS| = |BS|)

planimetria: Wydawało mi się, że środek okręgu opisanego na czworokącie jest punktem jednakowo odległych od wszystkich wierzchołków tego wielokąta, więc myślałam, że nie ma różnicy, które odległości porównam. W każdym razie dziękuję, tak rzeczywiście "działa"!

planimetria: *odległym

planimetria: Chyba się zbytnio pospieszyłam. Nie działa. |AS|=√(x−7)²+(3+4)²=√x²−14x+98 |CS|=√(x−6)²+(3−4)²=√x²−12x+37 |AS|=|CS| ⇔ √x²−14x+98=√x²−12x+37 ⇔ x=−30.5 Prawidłowa odpowiedź to S=(29,3)

Blee: A = (7, −4) C = (6, 5) więc dlaczego masz (3−4)²

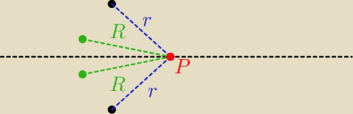
Blee: zauważ, że dla dowolnego umiejscowienia punktu P będzie zachodziły równości pokazane na rysunku (to wynika z tego, że punkt P leży na osi symetrii ), dlatego właśnie istotne jest sprawdzenie kiedy r = R

planimetria: Mój błąd. Rozumiem już. Bardzo dziękuję za pomoc.