prosta w przestrzeni Julia: Znajdź współrzędne punktu symetrycznego do punktu P₀ = (3, 0, 1) względem prostej

	x−5		y+1		z+2
		=		=
	2		1		3

Nie wiem, czy dobrze myślę... Z równania prostej mogę odczytać, że przechodzi przez punkt (5, −1, −2), dobrze rozumiem? Więc punktem symetrycznym do P₀ będzie po prostu P₀'(a, b, c), gdzie:

	(3, 0, 1)+(a, b, c)
(5, −1, −2) =
	2

Blee: no dobrze ... a dlaczego punkt (5, −1, −2) bierzesz pod uwagę ... a nie np. (10, 0, 1) ? Bądź jakikolwiek inny punkt na danej prostej

Blee: Ja bym to zrobił tak: 1) z równania prostej wyznaczasz wektor równoległy do tejże prostej 2) wektor ten jest niczym innym jak wektorem normalnym PŁASZCZYZNY prostopadłej do tejże prostej 3) wyznaczasz teraz tą płaszczyznę która będzie zawierać P₀ 4) wyznaczasz punkt przecięcia się prostej z tą wyznaczoną płaszczyzną 5) I to jest ten punkt, który Ty (nie mówiąc dlaczego) sobie przyjęłaś

Julia: Wzięłam ten punkt z ogólnego równania prostej:

x−x0		y−y0		z−z0
	=		=		więc prosta przechodzi przez (x0, y0, z0) o wektorze [a,
a		b		a

b, c]? Nie wiem jak zrobić to zadanie Twoim sposobem

jc: Płaszczyzna prostopadła do prostej (x,y,z)=(5,−1,−2)+t(2,1,3) przechodząca przez punkt (3,0,1): 2(x−3) + y + 3(z−1)=0 czyli 2x+y+3z=9. Punkt wspólny prostej i płaszczyzny: 2(5+2t)+(−1+t)+3(−2+3t)=9 14t=6, t=3/7, (x,y,z)=(41/7, −4/7, −5/7). Szukany punkt = 2(41/7, −4/7, −5/7) − (3,0,1) = ... Sprawdź rachunki.

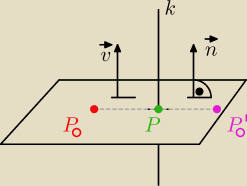
Julia: Rysunek, by lepiej to przyswoić, mam nadzieję że poprawny... Ok, i chyba zaczynam łapać, czyli 1) wektor równoległy do tej prostej to wektor kierunkowy = [2, 1, 3] 2) wektor normalny płaszczyzny prostopadły do niej = wektor kierunkowy prostej prostopadłej do płaszczyzny = [2, 1, 3] 3) Równanie płaszczyzny: A(x−x₀)+B(y−y₀)+C(z−z₀)=0. Płaszczyzna zawiera punkt P₀(3, 0, 1) i jej wektor normalny to [2, 1, 3], czyli równanie płaszczyzny wynosi: 2(x−3)+1(y−0)+3(z−1)=0 ⇒ 2x+y+3z−9=0 4) punkt wspólny prostej i płaszczyzny, to korzystam z równania parametrycznego (?) prostej tak jak @jc x = 5 + 2t, y = −1 + t, z = −2 + 3t Podstawiam (x, y, z) do równania płaszczyzny: 2(5+2t)+(−1+t)+3(−2+3t)−9=0 ⇒ t = 3/7 5) Punkt wspólny to: (5+2*3/7, −1+3/7, −2+3*3/7) = (41/7, −4/7, −5/7) P₀' = (a, b, c) (41/7, −4/7, −5/7) = ( (3, 0, 1) + (a, b, c) )/2 (82/7, −8/7, −10/7) − (3, 0, 1) = (a, b, c) ⇒ (a, b, c) = (61/7, −8/7, −17/7) = P₀' (Odp.) Więc wychodzi na to, że sposób, którym chciałam to zrobić

	(3, 0, 1)+(a, b, c)
(5, −1, −2) =		jest niepoprawny, bo wg tego wychodzi (7, −2, −5)...
	2

Czy może gdzieś zrobiłam błąd?

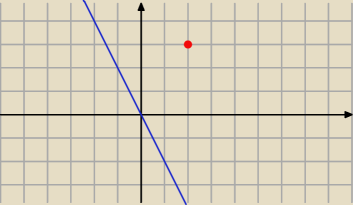
Blee: Sposób Twój był błędny bo wzięłaś "pierwszy lepszy" punkt leżący na tejże prostej. To tak jakbyś miała (na płaszczyźnie) analogiczne zadanie: znajdź współrzędne punktu symetrycznego do punktu P(2,3) względem prostej 2x + y = 0 i rozwiązując byś sobie wzięła punkt (1,2) (nie wiedzieć czego i dlaczego)

jc: Wektor (5,−1,−2)−(3,0,1) = (2,−1, −3) nie jest prostopadły do wektora (2,1,3). Punkt na prostej musi być tak wybrany, aby wektor łączący ten punkt z punktem (3,0,1) był prostopadły do prostej, czyli do wektora (2,1,3).

Julia: Rozumiem, dziękuję za pomoc