planimetria planimetria: Czworokąt ABCD jest wpisany w okrąg o środku w punkcie O. Wiedząc, że AD||BC, |BC|=|DC| oraz |<BAQ|=32^o, oblicz miary kątów wewnętrznych tego czworokąta.

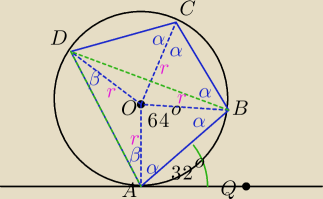ite: AD||BC, |BC|=|DC| trapez wpisany w okrąg → trapez równoramienny |DC|=|AB| |<ADB|=|<BAQ|=32^o || Miary kąta wpisanego opartego na danym łuku i kąta dopisanego wyznaczającego ten sam łuk są równe. |<AOB|=2|<ADB|=64^o w ΔAOB 180^o−64^o=116^o=2α |<ABC|=|<BCD|=2α=116^o |<DOA|=360^o−64^o−64^o−64^o=12^o ΔDOA równoramienny

	1
|<ADO|=|<DAO|=β=		12o=6o
	2

|<DAB|=|<ADC|=58^o+6^o=64^o

planimetria: BARDZO DZIĘKUJĘ!