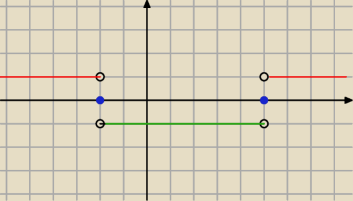
wykresy Krzysiek60: narysuj wykres funkcji f(x)= sgn(x²−3x−10 ) x₁+x₂=3 x₁*x₂=−10 z tego mam x₁=−2 x₂=5 Dla x∊{−2,5} =0 dla x∊(−∞,−2)U(5,∞) = 1 dla x∊((−2,5)=−1

Krzysiek60: Narysuj wykres takiej funkcji f(x)= sgn(−x²−4x+5)+sgn(−x²−x+6 ) −x²−4x+5=0 Δ= 36 x₁= 1 x₂= −5 bedzie tutaj x∊(−5,1)=1 x∊{−5, 1}=0 x∊(−∞ −5)U(1,∞)= −1 −x²−x+6=0 x₁=−3 x₂=2 dla x∊{−3,2} =0 dla x∊(−3,2)=1 dla x∊(−∞ −3)U(2,∞)=−1 Nie wiem jak teraz to polaczyc . Proszse z wytlumaczeniem dlaczego tak .

the foxi: dobry wieczór może narysuj oba wykresy w jednym układzie współrzędnych? odpowiedź nasunie się sama

the foxi: albo: dla x<−5 oba signumy przyjmują wartość −1, zatem dla x<−5 f(x)=−1−1=−2 dla x=−5 jeden signum przyjmuje wartość 0, drugi −1, więc f(−5)=0−1=−1 i teraz do kolejnego "zera": dla x∊(−5;−3) jeden signum przyjmuje wartość 1, a drugi −1, zatem f(x)=1−1=0 dla x=−3 jeden signum przyjmuje wartość 1, drugi 0, więc f(3)=1+0=1 i teraz do x=1... dla x∊(−3;1) oba są dodatnie, zatem f(x)=1+1=2 i tak dalej...

the foxi: szósta linijka, poprawka: zamiast f(3) powinno być f(−3)

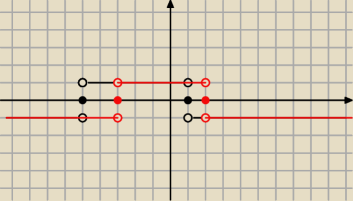
Krzysiek60: Czesc tak wyszlo na jednym W rozwiazaniu mam tak −2 dla x∊(−∞ −5)U(2.∞) −1 dla x∊{−5,2} 0 dla x∊(−5,−3)U(1,2) 1 dla x∊{−3,1} 2 dla x∊(−3,1) Nie rozumiem dlaczego tak a nie inaczej

Krzysiek60: O widzisz .

iteRacj@: foxi nie jesteś w klasie z łaciną ? ? ?

the foxi: cześć ite, nie

iteRacj@: to muszę coś dodać ze swojej branży (20:35) liceum − licea technikum − technika signum − ? ?

the foxi: hmm, Krzyśku, ja signum rozumiem jako funkcję, która zwraca znak wyrażenia w nawiasie (bo tak de facto jest) masz sgn, a w nich dwie funkcje kwadratowe wyrażenie jest równe 2 wtedy, gdy obie funkcje przyjmują wartość większą od zera 1 wtedy, gdy jedna jest dodatnia, druga się zeruje 0 wtedy, gdy obie funkcje mają wartości różnych znaków −1 wtedy, gdy jedna ma ujemne, druga się zeruje −2 wtedy, gdy obie funkcje przyjmują wartości ujemne tak na chłopski rozum

the foxi: signum − signa

the foxi: ach, racja, wiem już o co chodzi... "mały" błąd

Krzysiek60: ja tez tak to zrozumialem Tylko napisalem swoj post po twoim

iteRacj@: foxi to jeszcze dodam: jedno signum i znikam