Liczby zespolone Omikron: Naszkicuj na płaszczyźnie zespolonej te liczby z, które spełniają: 1) | z − 1 | + | z + i | = √2 2) | z − 3 | + | z + 3 | = 10

	z−1		π
3) Arg(		) =
	z+1		2

Mam problem z tymi trzema przykładami, prosiłbym o pomoc.

Adamm: |z−a|+|z−b| = c opisuje elipsę https://pl.wikipedia.org/wiki/Elipsa jej ogniska to a i b

Adamm: przepraszam, tu akurat nie będzie elipsy 1) to odcinek łączący 1 i −i 2) to zbiór pusty

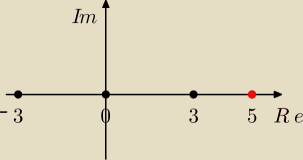
iteRacj@: czy w pkt 2/ to zbiór pusty? | z − 3 | + | z + 3 | = 10 | 5 − 3 | + | 5 + 3 | = 10

Adamm: Nie, to jednak elipsa Pomyliłem się

Omikron: Dlaczego w takim razie w 1 będzie to odcinek, a w 2 elipsa? Dalibyście jakąś wskazówkę jak do tego dojść?

Adamm: bo |z−a|+|z−b| ≥ |a−b| jeśli zachodzi równość, to to jest odcinek

iteRacj@: czy zbiór pusty byłby, gdyby c<|a−b| ?

Adamm: Lekkie deja vu ...

iteRacj@: owszem już o to kiedyś pytałam i jak trochę zapamiętałam, chociaż nie wszystko : )

Adamm: |z−a|+|z−b| = c c ≥ |a−b| to gdyby c<|a−b|, to nierówność nie byłaby spełniona

Omikron: Ok, dziękuję. To pozostaje jeszcze przykład 3.

Adamm:

	z−1
Arg(		) = π/2
	z+1

z−1
	∊ iR+
z+1

(z−1)(z*+1)
	∊ iR+
|z+1|2

(z−1)(z^*+1) ∊ iR₊ |z|²+z−z^*−1 ∊ iR₊ |z|=1 i Im(z)>0 to górna część okręgu o środku 0 i promieniu 1

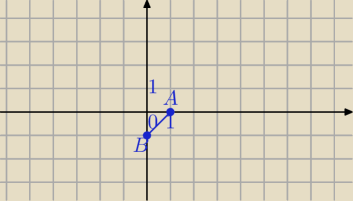
Mila: 1) 1) | z − 1 | + | z + i | = √2 A=(1,0), B=(0,−1) |AB|=√2 Zbiorem punktów jest odcinek AB.

Omikron: Dziękuję!

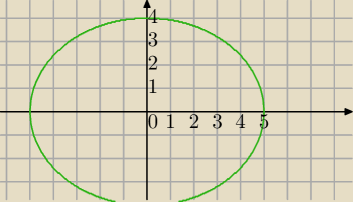
Mila: 2) | z − 3 | + | z + 3 | = 10 z₁=(3,0), z₂=(−3,0) |z₁z₂|=6 10>6 − zbiorem punktów będzie elipsa o ogniskach: (−3,0),(3,0) 2a=10, a=5 c²=a²−b² 3²=5²−b² b=4

x2		y2
	+		=1
25		16