funkcja kwadratowa z parametrem dusiamatmusia: Dla jakiś wartości parametru k równanie (k−2) x² +2kx+3 ma dwa różne miejsca zerowe należące do przedziału (−2;1)? 1 PRZYPADEK a>0 Δ>0 f(−2)>0 f(1)>0 p>−2 i p<1 2 PRZYPADEK a<0 Δ>0 f(−2)<0 f(1)<0 p>−2 i p<1 1 przypadek wyszedł sprzeczny przy 3 warunku. Mam problem, ponieważ w 2 przypadku wychodzi mi brak rozwiązań ze wszystkich warunków.

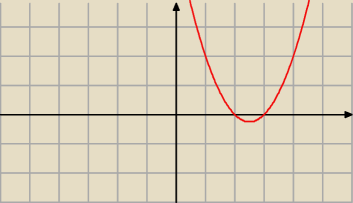
ICSP: Spójrz na taką funkcją kwadratową. Spełnia ona twoje warunki ale nie spełnia wymagań postawionych przez zadanie.

dusiamatmusia: Muszę dodać jakieś inne warunki? Nie za bardzo wiem jak to rozwiązać w takim razie.

ICSP: a = 0 − oczywisty Resztę załatwią warunki : 1^o Δ > 0 − gwarantuje dwa miejsca zerowe 2^o f(1)* a > 0 i f(−2) * a > 0 − umieszcza miejsca zerowe w jednym z trzech przedziałów 3^o −2 < x_w < 1 − znajduje odpowiedni przedział.

dusiamatmusia: Czy jak a będzie równe 0 to dalej będzie równanie kwadratowe o dwóch miejscach zerowych? Nie będzie wtedy funkcja liniowa?

ICSP: Funkcja liniowa która nie spełnia warunków zadania bo nie może mieć dwóch miejsc zerowych. To jest chyba oczywiste.

dusiamatmusia: Czyli nie ma takich wartości parametru k, które spełniałyby warunki zadania?

ICSP: Jeszcze raz. Przypadek a = 0 jest oczywisty. Dla a ≠ 0 podałem ci trzy warunki : 1^o , 2^o , 3^o. Trzeba je rozwiązać i znaleźć część wspólną.

dusiamatmusia: Teraz rozumiem, dzięki wielkie.