2 zadania Igor Z: Witam i proszę o pomoc Mam takie dwa zadania z którymi nie mogę sobie poradzić ♥ Wykaż,że w trójkącie prostokątnym kwadrat długości środkowej poprowadzonej z wierzchołka kąta prostego jest równy 1/5 sumy kwadratów długości dwu pozostałych środkowych ♦W prostokącie poprowadzono z przeciwległych wierzchołków odcinki prostopadłe które podzieliły przekątną na trzy równe części Wykaż ,że stosunek boków prostokąta jest równy √2

Mila:

	1
|CD|=		c
	2

	1		1		1		1
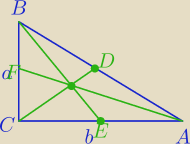
|BE|2=a2+(		b)2 , |AF|2=b2+(		a)2, |CD|2=(		c)2=		c2
	2		2		2		4

	1		1		1		5
|BE|2+|AF|2=a2+		b2+b2+		a2=c2+		(a2+b2)=		c2
	4		4		4		4

|CD|		1   c2 4		1
	=		=
|BE|2+|AF|2		5   c2 4		5

	1
|CD|2=		*(|BE|2+|AF|2)
	5

cnw

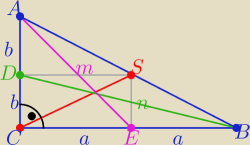Eta: |CS|²=a²+b² z tw, Pitagorasa w ΔCDB i w ΔCAE n²=b²+4a² m²=4b²+a² + −−−−−−−−−−−−−−−−−−−−−−

	m2+n2
m2+n2= 5a2+5b2 ⇒		=a2+b2= |CS|2
	5

c.n.w.

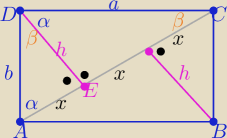Eta: 1/ rysunek i odpowiednie oznaczenia zgodne z treścią zadania Z podobieństwa trójkątów AED i CED z cechy (kkk)

h		2x
	=		⇒ h=x√2
x		h

	a		h		a
oraz		=		⇒		=√2
	b		x		b

======= c.n.w

pytam: Eta mam pytanie : czy udzielasz sie gdzies ? jakies korepetycje czy lekcje ? Bo z tak przeogromna wiedza troche marnujesz sie na forum (ktore niestety chyba odwiedza znacznie mniej osob niz kiedys). nie wiesz kto ja (chyba, ze jako moderator mozesz sprawdzic po IP; jesli tak to prosze bys tego nie ujawniala − dawno mnie nie bylo, mialem dluzsza przerwe od matematyki i wpadam teraz sporadycznie by przypomniec sobie to i owo i moze pomoc). Pozdrawiam