Nierówność z wartością bezwględną Kot-chromowany: Dzień dobry bardzo prosiłbym o rady w sposobie rozwiązywanie nierówności typu ||2x+5| − 6 | > 1 tzn. Chodzi mi dokładniej o jak najbardziej optymalny sposób rozwiązywania nierówności z wr.absolutną zawartą w innej.

xxx: ||2x+5| − 6| > 1 |2x+5| −6 > 1 v |2x+5| −6 < −1 |2x+5| > 7 v |2x+5| < 5 ... dalej chyba rozumiesz?

Kot-chromowany: Z tym że jest to sposób w którym dosyć łatwo o pomyłkę. A zastanawiam się czy nie dałoby się jakoś prościej np. przedziałami? Bo algebraicznie wychodzi x ⊂ (−niesk. , −6) U (−5,0) U (1 , +niesk.) i kontynuując Pana/Pani zapis jest to wytwór równań: |2x+5 | – 6 > 1 |2x+5| − 6 < −1 |2x+5|> 7 LUB |2x+5| < 5 2x+5 > 7 LUB 2x+5 < −7 2x+5 < 5 ORAZ 2x+5 > −5 2x<0 ORAZ 2x > −10 2x> 2 LUB 2x< −12 LUB x<0 ORAZ x>−5 x>1 LUB x< −6 Sumarycznie x ⊂ (−niesk. , −6) U (−5,0) U (1 , +niesk.) Ale czy jest opcja, żeby to to zapisać jakoś na zasadzie jeżeli |2x+5| ⊂ <0,6> to 6 − |2x+5| > −5 bo w tej drugiej opcji mam potem duży problem z zapisem

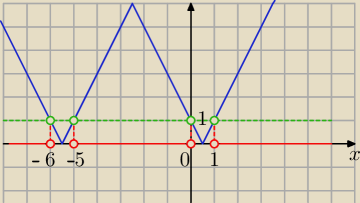
Eta: graficznie rysujesz wykresy: y=||2x+5|−6| i y=1 Odczytujesz kiedy niebieski wykres znajduje się nad wykresem zielonym Odp: x∊(−∞, −6)u(−5,0)U(1,+∞) ========================

Kot-chromowany: Dziękuje za pomoc