sześciokąt walduś: Dany jest sześciokąt foremny ABCDEF wewnątrz którego wybrano punkt P Wykaż,ze suma pól trójkatów AFP, BCP i DEP jest równa połowie pola sześciokąta ABCDEF

walduś: up

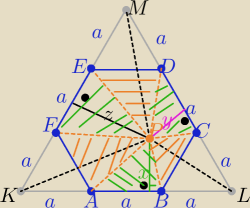
Eta: Umieszczam sześciokąt w trójkącie równobocznym o boku 3a

	9a2√3
to P(ΔKLM)=
	4

P₁=P(ABP)=P(KAP)=P(BLP) bo mają wspólną wysokość x i podstawy a analogicznie P₂=P(LPC)=P(CPD)=P(DMP) i P₃=P(KFP)=P(EFP)=P(EMP) zatem

	3a2√3
P(KLM) = 3P1+3P2+3P3 ⇒		=P1+P2+P3
	4

	a2√3		3a2√3
P(ABCDEF)= 6*		=
	4		2

	1
to P1+P2+P3=		P(ABCDEF)
	2

	1
więc i P(AFP)+P(BCP)+P(DEP)=		P(ABCDEF)
	2

c.n.w

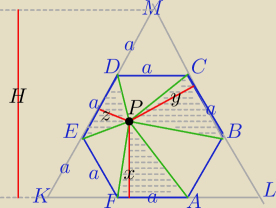
Mila: II sposób 1)

1		3*a2√3
	PABCDEF=
2		4

2) Suma odległości punktu P od boków ΔKLM jest równa:

	3a√3		3a√3
H=		⇔ x+y+z=
	2		2

3) Suma pól trójkątów AFP, BCP i DEP :

	1		1		1
P=		a*x+		a*y+		a*z=
	2		2		2

	1		1		3a√3
=		a*(x+y+z)=		a*
	2		2		2

	3a2√3
P=
	4

cnw =============