Równania Pol: Rozwiąż nierówności a)log_0,2(x+2)+1≤−log_0,2(2x−5) b)√12−6sinx≥2sinx+2

Bleee: Założenia chociaż zrobiłaś?

Eta: A skąd wiesz,że to dziewczyna ?

Pol: Do pierwszego tak

Mila: 1) log_0,2(x+2)+1≤−log_0,2(2x−5)

	5
x+2>0 i 2x−5>0⇔x>
	2

log_0,2(x+2)+log_0,2(2x−5)≤−1

	2
log0.2[(x+2)*(2x−5)]≤log0.2(		)−1⇔
	10

2x²−x−10≥5

	5
2x2−x−15≥0 i x>
	2

Δ=121

	1−11		1+11		5
[x=		lub x=		] i x>
	4		4		2

	5
x=−		lub x=3
	2

	5		5
[x≤−		lub x≥3] i x>		⇔
	2		2

x≥3 ========

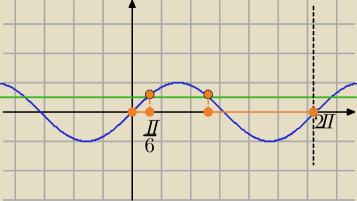
Mila: 2) √12−6sinx≥2sinx+2 12−6sinx≥0 12≥6sinx sinx≤2 spełnione dla każdego x∊R Obustronnie podnosimy do kwadratu , 2sinx+2≥0 12−6sinx≥4sin²x+8sinx+4 4sin²x+14sinx−8≤0 /:2 2sin²x+7sinx−4≤0 sinx=t, |t|≤1 2t²+7t−4≤0 Δ=81

	−7−9		−7+9		1
t=		=−4 lub t=		=
	4		4		2

	1
[−4≤t≤		] i −1≤t≤1⇔
	2

	1
−1≤t≤
	2

	1
sinx≥−1 i sinx≤
	2

Odczytaj rozwiązanie.

Jerzy: Dwie niezawodne dziewczyny od wielu lat Pozdrawiam serdecznie: )

Eta:

Mila: Też pozdrawiam Znowu jesteś czarny?

Eta: Pewnie opalał się w Afryce

Jerzy: Nie, ale dwa tygodnie temu byłem w Chicago i poznałem przesympatycznego Nepalczyka, a dzisiaj mamy problem z piratami ( być może z Nepalu).

Mila: Zgubne skutki podejrzanych znajomości