:c: Odcinek AB A(−2;1) B(6;1) jest podstawa Δ rownoramiennego
Wyznacz C jesli nalezy do y=x+2
30 paź 18:43
Riczard: D= środek AB
D=(x;y)
x=(−2+6)/2=2
y=(1+1)/2=1
D=(2;1)
AB
1=−2a+b
1=6a+b
−2a+b=6a+b
−2a−6a=0
a=0
1=b
y=1
prostopadła do AB;
a=0
x=2
punkt przecięcia sie prostych
x=2 i y=x+2 y=2+2=4
C=(2,4)
30 paź 18:48
:c: Rozumiem do momentu wyznaczenia osi symetrii ale dalej niewiem skad sie wziely proste AC i BC
30 paź 18:56
Krzysiek60: Bo jak poprzednim razem nie zrobiles rysunku i nawet nie raczyles odpowiedzec czy rozumiesz
Wiec teraz domyslaj sie sam .
30 paź 18:58
:c: mam rysunek od poczatku i co tak agresywnie krzysiu
30 paź 18:59
:c: ale jakos nie widze opcji wyznaczenia AC i BC dlatego prosze o wytlumaczenie
30 paź 18:59
Eta:
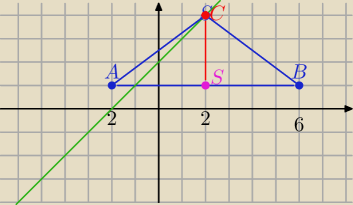
S( 2,1) AB :y=1 to CS ⊥ AB i S∊ CS ⇒ CS : x=2
C∊ (y=x+2) to C( x,x+2) ⇒ C(2,2+2) ⇒
C(2,4)
i po b
ólu
30 paź 19:10
:c: boze czemu jestem taki slepy
30 paź 19:15
Krzysiek60:
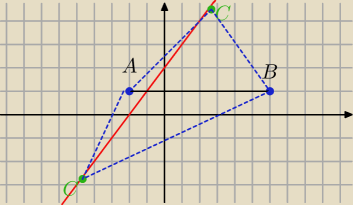
Przykladowy punkt C ktory lezy na prostej y=x+2 musi byc rownoodlegly zarowno od punktu A
=(−2,1)
jak i punktu B=(6,1) bo to trojkat rownoramienny Musi byc AC=BC
Z rysunku widac ze beda takie dwa punkty
Punkt C ma wspolrzene C=(x,x+2)
Masz wzor na dlugosc odcinka
d=
√(x2−x1)2+(y2−y1)2
|Dlugosc odcinka AC
|AC|=
√(x+2)2+(x+2−1)2
dlugosc odcinka BC
|BC|=
√(x−6)2+(x+2−1)2
AC=BC
√(x+2)2+(x+1)2=
√(x−6)2+(x+1)2 do potegi drugiej zeby pozbyc sie pierwiastkow
(x+2)
2+(x+1)
2= (x−6)
2+(x+1)
2
Rozwiz to rownanie
Potem wyliczone x wstaw do rownia y=x+2 i wylicz wspolrzedne y
Imiona piszemy z duzej litery (szacunek do drugiego czlowieka
30 paź 19:24
Eta:
Jaki ten drugi punkt ?

30 paź 19:26
Krzysiek60: Dobry wieczor

Zapomnialem ze zawsze jest
Patrz punkt pierwszy
Eta Nie liczylem tego .
30 paź 19:29
Eta:
Witam

Widzę,że lubisz podróżować .. z Wrocławia do Londynu przez Kair

na maturze na taką wycieczkę .. nie ma czasu

30 paź 19:33
 S( 2,1) AB :y=1 to CS ⊥ AB i S∊ CS ⇒ CS : x=2
C∊ (y=x+2) to C( x,x+2) ⇒ C(2,2+2) ⇒ C(2,4)
i po bólu
S( 2,1) AB :y=1 to CS ⊥ AB i S∊ CS ⇒ CS : x=2
C∊ (y=x+2) to C( x,x+2) ⇒ C(2,2+2) ⇒ C(2,4)
i po bólu
 Przykladowy punkt C ktory lezy na prostej y=x+2 musi byc rownoodlegly zarowno od punktu A
=(−2,1)
jak i punktu B=(6,1) bo to trojkat rownoramienny Musi byc AC=BC
Z rysunku widac ze beda takie dwa punkty
Punkt C ma wspolrzene C=(x,x+2)
Masz wzor na dlugosc odcinka
d=√(x2−x1)2+(y2−y1)2
|Dlugosc odcinka AC
|AC|= √(x+2)2+(x+2−1)2
dlugosc odcinka BC
|BC|= √(x−6)2+(x+2−1)2
AC=BC
√(x+2)2+(x+1)2=√(x−6)2+(x+1)2 do potegi drugiej zeby pozbyc sie pierwiastkow
(x+2)2+(x+1)2= (x−6)2+(x+1)2
Rozwiz to rownanie
Potem wyliczone x wstaw do rownia y=x+2 i wylicz wspolrzedne y
Imiona piszemy z duzej litery (szacunek do drugiego czlowieka
Przykladowy punkt C ktory lezy na prostej y=x+2 musi byc rownoodlegly zarowno od punktu A
=(−2,1)
jak i punktu B=(6,1) bo to trojkat rownoramienny Musi byc AC=BC
Z rysunku widac ze beda takie dwa punkty
Punkt C ma wspolrzene C=(x,x+2)
Masz wzor na dlugosc odcinka
d=√(x2−x1)2+(y2−y1)2
|Dlugosc odcinka AC
|AC|= √(x+2)2+(x+2−1)2
dlugosc odcinka BC
|BC|= √(x−6)2+(x+2−1)2
AC=BC
√(x+2)2+(x+1)2=√(x−6)2+(x+1)2 do potegi drugiej zeby pozbyc sie pierwiastkow
(x+2)2+(x+1)2= (x−6)2+(x+1)2
Rozwiz to rownanie
Potem wyliczone x wstaw do rownia y=x+2 i wylicz wspolrzedne y
Imiona piszemy z duzej litery (szacunek do drugiego czlowieka

 Zapomnialem ze zawsze jest Patrz punkt pierwszy
Eta Nie liczylem tego .
Zapomnialem ze zawsze jest Patrz punkt pierwszy
Eta Nie liczylem tego .
 Widzę,że lubisz podróżować .. z Wrocławia do Londynu przez Kair
Widzę,że lubisz podróżować .. z Wrocławia do Londynu przez Kair  na maturze na taką wycieczkę .. nie ma czasu
na maturze na taką wycieczkę .. nie ma czasu 