opisywanie funkcji
Tomal: funckja f okreslona jest wzorem f(x) =
3x2 +1
Wyznacz zbior wartosci funkcji f
podaj przedzial liczbowy w ktorym funkcja jest malejaca
Dziedzina oczywiscie R
Prosiłbym o rozwiazanie bez delty, granicy czy czegoś takiego bo tego jeszcze nie miałem

w moim podgladzie jest tam cyba −3 ale chodzi o 3

29 paź 18:40
Krzysiek60: Robie to tylko dla siebie
Ze wzoru widac ze funkcja jest parzysta (nie ma co liczyc
Teraz zbior wartosci
3−s(x
2+1)=0
3−sx
2−s=0
−sx
2−s+3=0
dla s=0 f(0)=3
dla s≠0 to rownanie ma rozwiazanie jesli Δ>0
Δ=(−s)
2−4*(−s)*3=s
2+12s = s(s+12)>0 wiec s∊(−
∞,−12)U(0,
∞)
Jak analizowac ten wynik ?
29 paź 21:14
the foxi:
sx2+s−3=0
Δ=−4s(s−3)
Δ>0 ⇔ s∊(0;3)
ostatecznie s∊(0;3]
29 paź 21:21
jc: | | 3 | |
Czy to tam jest f(x)= |
| ? |
| | x2+1 | |
Funkcja maleje na przedziale [0,
∞).
Krzysiek, f(R)=(0,3]. Czy to nie jest oczywiste?
29 paź 21:23
the foxi:
fakt, w tym przykładzie można polegać na intuicji
mianownik jest zawsze większy bądź równy 1
zatem największa wartość funkcji jest wtedy, gdy x2+1=1, czyli fmax(x)=3
a najmniejsza, gdy licznik dąży do nieskończoności, czyli cały ułamek dąży do zera
czyli, tak jak pisze jc, f(R)=(0,3]
29 paź 21:27
Krzysiek60: Witam
jc i
the foxi 
O tym wzrastaniu i maleniu funkcji to wiedzialem
Tylko dlaczego foxi tak policzyles delte ?
29 paź 21:35
Krzysiek60: Oczami wyobrazni widzialem tam przy sx

Dlatego wyszlo mi zle

29 paź 21:39
the foxi:
hej

−sx
2−s+3=0
a=−s, b=0, c=3−s
Δ=b
2−4ac=−4*(−s)(3−s)=4s(3−s)=−4s(s−3)
typowe niedopatrzenie, za współczynnik b wziąłeś część wyrazu wolnego

29 paź 21:39
Eta:
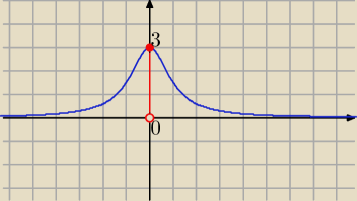
29 paź 21:44
Krzysiek60: Eta 
ja ten wykres mialem przed oczami .Powaznie .
Spatolilem delte .
29 paź 21:45
 w moim podgladzie jest tam cyba −3 ale chodzi o 3
w moim podgladzie jest tam cyba −3 ale chodzi o 3 
 O tym wzrastaniu i maleniu funkcji to wiedzialem
Tylko dlaczego foxi tak policzyles delte ?
O tym wzrastaniu i maleniu funkcji to wiedzialem
Tylko dlaczego foxi tak policzyles delte ?
 Dlatego wyszlo mi zle
Dlatego wyszlo mi zle 
 −sx2−s+3=0
a=−s, b=0, c=3−s
Δ=b2−4ac=−4*(−s)(3−s)=4s(3−s)=−4s(s−3)
typowe niedopatrzenie, za współczynnik b wziąłeś część wyrazu wolnego
−sx2−s+3=0
a=−s, b=0, c=3−s
Δ=b2−4ac=−4*(−s)(3−s)=4s(3−s)=−4s(s−3)
typowe niedopatrzenie, za współczynnik b wziąłeś część wyrazu wolnego 

 ja ten wykres mialem przed oczami .Powaznie .
Spatolilem delte .
ja ten wykres mialem przed oczami .Powaznie .
Spatolilem delte .