pomocy!
Paulina: 1. W urnie znajdują się kule białe i czarne. Kul białych jest 3 razy wiecej niz czarnych.
Oblicz ile jest kul w urnie, jesli przy jednoczesnym losowaniu dwóch kul prawdopodobieństwo
otrzymania kul o roznych kolorach jest wieksze od 9/22?
12 lut 19:18
nestor:
n −− ilość czarnych
3n −−− ilość białych , n ≥1
r−m : 4n kul
| | 3n2 | | 9 | |
to: |
| > |
| /* 23........ i n skaracamy
|
| | 2n(4n−1) | | 22 | |
11n > 12n −3
n <3 i n ≥1 to n€ <1,3)
więc n= 1 v n= 2
dla n=1 mamy 1 kulę czarną i 3 kule białe ,to razem w urnie jest 4 kule
dla n= 2 mamy 2 kule czarne i 6 kul białych , to razem w urnie jest 8 kul
Odp: w urnie mogą być: 4 kule lub 8 kul.
12 lut 20:33
Paulina: dziękuję

12 lut 20:36
Ola:
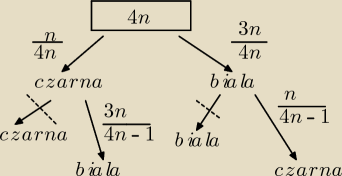
Równanie tego prawdopodobieństwa jest inne niż napisałaś wcześniej.
Napisze wszystko od początku, aby się nie pomylić.
n − kule czarne
W urnie znajduje się 3n − kul białych i n − kul czarnych, czyli wszystkich 4n. Można to ładnie
rozrysować na drzewku stochastycznym, czasami to pomaga, choć zajmuje dużo czasu.
Interesują Nas tylko te losowania, w których wylosujesz dwie kule o różnych kolorach. Są dwa
takie przypadki.
| n | | 1 | | 3n | | 3 | |
| = |
| , a |
| = |
| , z tego już może wynikać, że są 4 kule (1 czarna i 3 |
| 4n | | 4 | | 4n | | 4 | |
białe)
| n | | 3n | | 3n | | n | | 9 | |
| * |
| + |
| * |
| > |
|
|
| 4n | | 4n−1 | | 4n | | 4n−1 | | 22 | |
Założenie: 16n
2 − 4n ≠ 0, czyli n∊ ℕ\{0; 4}
33n
2 > 36n
2 − 9n
−3n
2 + 9n > 0
Δ = 81, czyli
√Δ = 9
n
1 = 3
n
2 = 0 (nie spełnia założenia)
Z tego wynika, że kul może być także 12. Pisałaś, że odpowiedź to 4 lub 8 kul, może gdzieś
zrobiłam błąd.
12 lut 21:48
Bogdan:
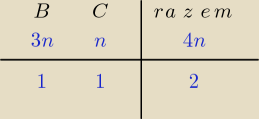
Zamiast czasochłonego drzewka, wygodniej jest sporządzić taką prostą tabelkę.
12 lut 21:56
Dżagalaga: Zadanie rozwiązałem i również wyszło mi, że kul jest 12 =)
12 lut 21:56
molo: straszne
3 maj 22:59

 Równanie tego prawdopodobieństwa jest inne niż napisałaś wcześniej.
Napisze wszystko od początku, aby się nie pomylić.
n − kule czarne
W urnie znajduje się 3n − kul białych i n − kul czarnych, czyli wszystkich 4n. Można to ładnie
rozrysować na drzewku stochastycznym, czasami to pomaga, choć zajmuje dużo czasu.
Interesują Nas tylko te losowania, w których wylosujesz dwie kule o różnych kolorach. Są dwa
takie przypadki.
Równanie tego prawdopodobieństwa jest inne niż napisałaś wcześniej.
Napisze wszystko od początku, aby się nie pomylić.
n − kule czarne
W urnie znajduje się 3n − kul białych i n − kul czarnych, czyli wszystkich 4n. Można to ładnie
rozrysować na drzewku stochastycznym, czasami to pomaga, choć zajmuje dużo czasu.
Interesują Nas tylko te losowania, w których wylosujesz dwie kule o różnych kolorach. Są dwa
takie przypadki.
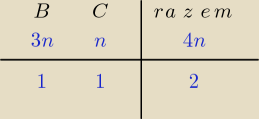 Zamiast czasochłonego drzewka, wygodniej jest sporządzić taką prostą tabelkę.
Zamiast czasochłonego drzewka, wygodniej jest sporządzić taką prostą tabelkę.