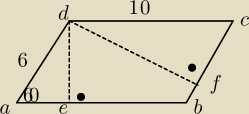
 Boki równoległoboku ABCD mają długość 6 i 10, a kąt ostry ma miarę 60o. Punkty E i F są
spodkami wysokości równoległoboku poprowadzonymi z wierzchołka.
Uzasadnij, że na czworokącie EBFD można opisać okrąg.
Zauważam, że ΔDEB i ΔDFB mają wspólną przeciwprostokątną, która jest średnicą okręgu opisanego
na każdym z nich. Okręgi się pokrywają, czyli okrąg tren jest opisany na czworokącie EBFD. Ale
czy to wystarczy?
Boki równoległoboku ABCD mają długość 6 i 10, a kąt ostry ma miarę 60o. Punkty E i F są
spodkami wysokości równoległoboku poprowadzonymi z wierzchołka.
Uzasadnij, że na czworokącie EBFD można opisać okrąg.
Zauważam, że ΔDEB i ΔDFB mają wspólną przeciwprostokątną, która jest średnicą okręgu opisanego
na każdym z nich. Okręgi się pokrywają, czyli okrąg tren jest opisany na czworokącie EBFD. Ale
czy to wystarczy?
| 1 | ||
R= | √76 | |
| 2 |