Znajdź równanie prostej uczeń: Znajdź równanie prostej k przechodzącej przez punkt P(1, −1) wiedząc, że odległość tej prostej od punktu Q (8, −2) jest równa 5 Prosze o wskazówki

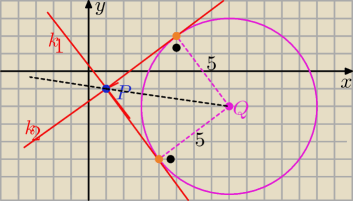
nestor: tymi prostymi są : styczne do okręgu o: ( x−8)² +(y+2)²= 25 poprowadzone z punktu P 1) sposób k: y= ax +b i P€ k to −1=a+b => b= −1−a rozwiąż układ równań tej prostej z okręgiem nałóż warunek : Δ= 0 i wyznacz "a" i "b" 2) sposób: odległość punktu Q od prostej k : d= 5 k: ax − y +b=0 Q( 8,−2) d= 5

	|8a+2 +b|
d=		= 5
	√a2+1

podstaw za b= −1−a i dokończ odp : k₁: y = −³₄x −⁷₄ k₂: y= ⁴₃x +¹₃

nestor: Poprawiam chochlika odp: k₁: y= ³₄x−⁷₄ k₂: y= −⁴₃x+¹₃

uczeń: nie powinno być d= ^{|8A + 2B + C|}_√A² + B²

uczeń: coś mi nie wyszło w każdym razie mamy równanie prostej Ax + By + C i skąd wiesz, że B = 0

uczeń: tzn. B = 1, a nie 0