trapez dowod ewa: W trapezie ABCD poprowadzono prostą równoległą do podstawy i przechodzącą przez pkt przecięcia przekątnych. Prosta przecina boki nierównoległe trapezu w punktach E i F. Wykaż, że |EF|=

	2ab
		, gdzie a=|AB|, b=|CD|
	a+b

ewa: pomoze ktos:(

Bogdan:

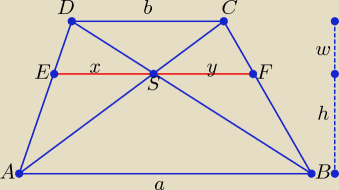
	a		h		aw
Z podobieństwa trójkątów: ABS i CDS:		=		⇒ h =
	b		w		b

	a		h + w		aw
Z podobieństwa trójkątów: ABD i ESD:		=		⇒ x =
	x		w		h + w

	a		h + w		aw
Z podobieństwa trójkątów: ABC i SFC:		=		⇒ y =		= x
	y		w		h + w

	aw		b		2abw		2ab
x + y = x + x = 2x = 2 *		*		=		=
	aw   + w b		b		w(a + b)		a + b

	2ab
|EF| =		, jest to średnia harmoniczna długości podstaw trapezu.
	a + b

ewa: Dziekuje za pomoc

x:

	a		h
skąd wiemy, że		=		− wiem pisze, że z podobieństwa trójkątów, ale te odcinki
	b		w

są zaznaczone poza trapezem, ewentualnie mogą to być wysokości, chodzi mi o to jak to uzasadnić, że stosunek a do b i h do w jest ten sam?

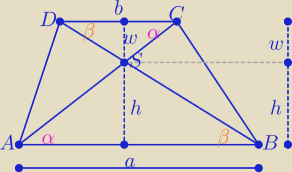
Eta: Co w tym trudnego? Z podobieństwa trójkątów ABS i DCS z cechy (kkk)

a		w
	=
b		h

Jasne?

x: ja to ogólnie rozumiem, ale nie wiem jak to uzasadnić, bo z podobieństwa, zazwyczaj wnioskujemy, że stosunki BOKÓW trójkątów są równe, ale jak uzasadnić, że ta sprawa ma się tak samo z wysokościami.

x:

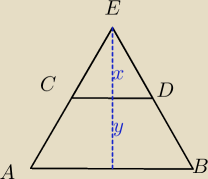
	x		|CD|
no nawet na takim prostszym przykładzie, jak pokazać, że		=		?
	y		|AD|

Eta: Jeżeli trójkąty są podobne w skali k>0 to i stosunki : nie tylko odpowiednich boków ale również odpowiednich wysokości i odpowiednich środkowych i..... są równe k

x: okej, dziękuje