relacje, minoranty, majoranty, el min max asdf: Dana jest relacja R = (R², grR, R²) (x, y) R (x', y') ⇔ x ≤ x' ∧ y ≤ y' Znajdz zbiory minorant, majorant, kresy, elementy min, max, najwieksze i najmniejsze dla zbioru: b = { (x, y): x² + y² ≤ 9}

math: spróbuj to narysować np. klasę abstrakcji dla punktu (0.0)

math: które punkty płaszczyzny sa w relacji z tym punktem?

asdf: To jest okrąg w srodku 0,0 o promieniu 3 To klasa abstrakcji dla (0;0) będą wszystkie punkty o wspolrzednej x ≥ 0 oraz y ≥ 0, czyli pierwsza ćwiartka cala, tak?

asdf: minoranty, majoranty, kresy mam teraz elementy min, max, najwieksze i najmniejsze ktoś podpowie?

iteRacj@: Mam wątpliwości co do klas abstrakcji podanej relacji. Czy to jest relacja symetryczna? Czy z tego że (x, y) R (x', y') wynika że (x', y') R (x, y)? Jeśli (x ≤ x' ∧ y ≤ y') to z tego nie wynika (x' ≤ x ∧ y' ≤ y) ? ?

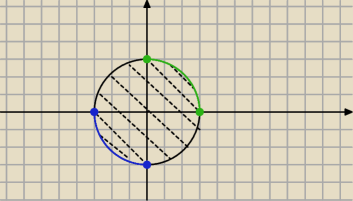
Pytający: Zgadza się Iteracjo, to częściowy porządek, a nie relacja równoważności, więc nie ma tu mowy o klasach abstrakcji. Math coś namieszał. Asdf, na rysunku zaznaczyłem elementy minimalne i maksymalne. Elementy najmniejszy i największy nie istnieją.

asdf: Pytający Mógłbys dodac słowa komentarza do el. min max najwiekszego i najmniejszego? Odpowiedź jest dobra, ale skąd się to wzięło

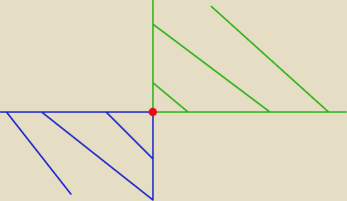
Pytający: To taki rysunek dorzucę: dla dowolnego punktu p=(x_p,y_p)∊ℛ² i dla każdego punktu w∊{(x,y)∊ℛ²: x_p≤x ∧ y_p≤y} (punkt p też należy do tego zbioru) zachodzi pRw, znaczy według tego porządku (relacji R) punkt p jest "mniejszy lub równy" od w. Łopatologiczniej: wszystkie punkty nie na lewo i nie w dół są większe lub równe od danego punktu. Znaczy jeśli nie ma już w danym zbiorze żadnego punktu na prawo lub do góry (zielony zbiór jest wtedy jednoelementowy, jedynie p do niego należy), to ów punkt p jest elementem maksymalnym (nie ma żadnego "większego" od niego). Podobnie dla dowolnego punktu p=(x_p,y_p)∊ℛ² i dla każdego punktu m∊{(x,y)∊ℛ²: x≤x_p ∧ y≤y_p} (punkt p też należy do tego zbioru) zachodzi mRp, znaczy według tego porządku (relacji R) punkt p jest "większy lub równy" od m. Znaczy jeśli nie ma już w danym zbiorze żadnego punktu na lewo lub na dół (niebieski zbiór jest wtedy jednoelementowy, jedynie p do niego należy), to ów punkt p jest elementem minimalnym (nie ma żadnego "większego" od niego). Elementy największy/najmniejszy nie istnieją, bo jeśliby istniały to byłyby odpowiednio jedynym elementem maksymalnym/minimalnym (a tych jest nieskończenie wiele).

asdf: A gdzie w tym rozumowaniu jest zbiór B?

Pytający: "Znaczy jeśli nie ma już w danym zbiorze (...)"

asdf: Aaaaaaa, troche sie wyjasnilo, dzieki