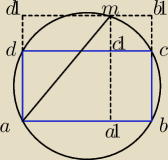
s plan: Na prostokącie ABCD opisano okrąg o środku w punkcie O. Wykaż, że suma kwadratów odległości dowolnego punktu M należącego do okręgu od czterech boków prostokąta jest stała i równa kwadratowi długości przekątnej AC tego prostokąta. Wiem, że odległościami punktu M od odpowiednich boków prostokąta są odcinki MA1, MB1, MC1, MD1, gdzie |MA1|=|MD1| i |MB1|=|C1C|, ale co dalej? Jakiś pomysł?

plan: ?

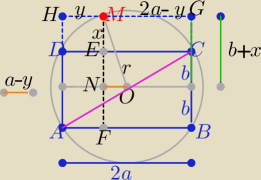
Eta: Dane na rysunku .......................... Mamy wykazać ,że : (*) |ME|²+|MF|²+|MG|²+|MH|²= |AC|² z tw. Pitagorasa: w ΔABC |AC|²=4(a²+b²) = 4r² w ΔONM : (b+x)²+(a−y)²=r²= a²+b² x²+y²−2ay+2bx=0 to lewa strona naszej równości (*) L=x²+₍x+2b)²+(2a−y)²+y² = .................... = 4(a²+b²)= |AC|² c,n,w

plan: skąd wziął się zapis: x²+y²−2ay+2bx=0?

Eta: W ΔONM : b²+2bx+x²+a²−2ay+y²=a²+b² ⇒ x²+y²−2ay+2bx=0

Eta: Czy już jasne?

plan: Zupełnie nie wiem skąd to się wzięło.

Eta: W ΔONM : |OM|=r = a²+b² , |MN|=b+x , |ON|=a−y z tw. Pitagorasa w tym trójkącie |MN|²+|ON|²= |OM|² i działaj .......... "zobaczysz skąd to się wzięło "

plan: Okej, już rozumiem, dziękuję. Jeszcze ostatnie pytanie: w jaki sposób z postaci x²+y²−2ay+2bx=0 przeszliśmy do x²+(x+2b)²+(2a−y)²+y²? (post z 14:28)

plan: Jakim cudem L=x²+(x+2b)²+(2a−y)²+y² = .................... = 4(a²+b²)?

Eta: Wykonaj potęgowanie , redukcję wyrazów i zobaczysz to o co pytasz Widzę,że chcesz wszystko mieć "na tacy" + jeszcze do picia schłodzoną colę

plan: O ludzie, faktycznie, gdzie ja mam mózg. Wcale nie chcę mieć na tacy. Po prostu nie rozumiem, więc pytam. Chyba dzisiejszy dzień nie jest mój − skoro zadania z podstawy sprawiają problem, musi być źle. Przepraszam najmocniej i dziękuję

Eta: łap

plan: Przyda się. Również

Eta: