wykaż że wykaze: W trójkącie równoramiennym ABC mamy |AC|=|BC|=4√3. Wysokość poprowadzona na postawę trójkąta jest równa odcinkowi łączącemu środek podstawy ze środkiem ramienia trójkąta. Uzasadnij, że sin(<ACB)=√3sin(<CAB)

wykaze: ?

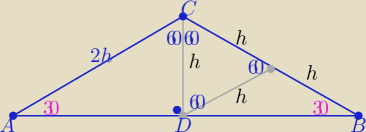
Eta: Taki rys. wystarczy ? 2h=4√3 , h=2√3 sin120^o = √3sin30^o

√3		√3
	=
2		2

c.n.w

an: Wszystko się zgadza, tylko na jakiej podstawie ten rysunek ?

Eta: Zapomniałam oznaczyć punkt F jako środek boku BC ΔDCF −− równoboczny ( z treści zadania )

an: "ΔDCF −− równoboczny ( z treści zadania )" równoramienny tak, równoboczny na jakiej podstawie CF=h Czy mam jakieś zamglenia

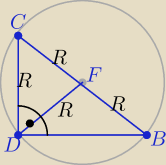
Eta: Środkowa DF poprowadzona z wierzchołka kąta prostego ma długość R |BC|=2R i |DC|=R =|DF| z treści zadania ΔDFC −−− równoboczny Ja oznaczyłam R jako h

Eta: Mila ja sobie też dam radę w wytłumaczeniu !

Mila: Przepraszam, myślałam , że już nie ma Cię na forum Pozdrawiam.

Eta: Też pozdrawiam

an: