rozwiązanie równania walec: −8* (¹₄)^4(sinπx)2 +6(¹₄)^2(sinπx)2 −1 >0 w |x|≤1 oczywiście podstawienie itp wychodzi : t∊(1/4,1/2) 1/4 dla x=−1/4 , 1/4 ,3/4 , 5/4 1/2 dla x=−1/6 , 1/6 ,5/6 , 7/6 no i teraz nie wiem jak napisac finalna odpowiedz x∊() (¹₄)^2(sinπx)2 jest okresowo malejąca i rosnąca i wg mnie odp to x∊(−1/4,−1/6)U(1/6,1/4)U(3/4,5/6) czy dobrze myślę ?

Mila: Tam jest ?

	1		1
−8*(		)4*(sinπx)2+6*(		)2*(sin(πx)2−1>0
	4		4

walec: tak Mila, sorki nie było mnie

walec: teraz znowu mam równanie gdzie t=log₍¹₂) sin ^x₂ //podstawa 1/2 wykladnik sinx/2 t∊(−∞,1/2)U(1,+∞) no i bez problemu potrafie rozwiazac t=1/2 i t =1 ale nie wiem jak mam przejsc z t∊(−∞,1/2)U(1,+∞) na x∊() help ktoś

walec: może ktos jednak poomoze ?

Mila: Jutro Dobranoc. Tylko jeszcze napisz , czy dziedziną pierwszej jest zbiór x: |x|<1 A drugie równanie jakie jest?

walec: w sumie nie chodzi o równania konkretnie, chodzi mi tylko jak przejść na x, tylko o ten mechanizm, całe równanie jest nie istotne, a w pierwszym tak |x|<1. I będę wdzieczny jutro Dobranoc

walec: ponawiam

Jerzy:

	1		1		1
(		)2(sinπx)2 > (		)1 ⇔ 2(sinπx)2 < 1 ⇔ (sinπx)2 <		⇔
	4		4		2

	√2		√2
⇔ −		< sinπ <
	2		2

	1
podobnie dla: t <
	2

Jerzy: Tam miało być oczywiście sinπx w przedostatniej linijce.

Jerzy: W drugim: log_0.5sin(x/2) < 1/2 ⇔ log_0.5sin(x/2) < log_0.5√1/2

	√2
⇔ sin(x/2) >
	2

Mila:

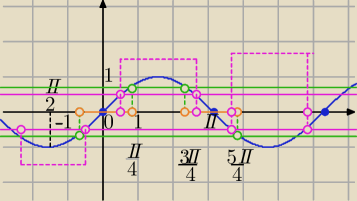
	1
t=(		)2*(sin(πx)2
	4

Dwie nierówności:

	1		1
t>		∧ t<		⇔
	4		2

	1		1		1		1
(1) (		)2*(sin(πx)2>(		)1 ∧ (2) (		)2*(sin(πx)2<(		)1 ∧
	4		4		4		2

|x|<1⇔ ad(1)

	√2
2*(sin(πx)2<1⇔|sin(πx)|<		∧ |x|<1
	2

	√2		√2
−		<sin(πx)<
	2		2

	π		π		3π		5π
−		<πx<		/:π lub		+2kπ<sin(πx)<		+2kπ
	4		4		4		4

	1		1		3		5		3
−		<x<		lub		<x<		⇔		<x<1 dla k=0 lub
	4		4		4		4		4

	5		3
dla k=−1 −		<x<−		⇔
	4		4

	3
−1<x<−
	4

Czyli z (1) mamy tak:

	3		1		1		3
−1<x<−		lub −		<x<		lub		<x<1
	4		4		4		4

======================================= ∧ Ad(2) nad różową linią lub pod różową linią 4(sin(πx))² >1

	1
|sin(πx)|>
	2

π		5π		7π		11π
	+2kπ<πx<		+2kπ lub		+2kπ<πx<
6		6		6		6

	1		5		7		11
k=0		<x<		lub		<x<		nie odpowiada zał.
	6		6		6		6

	5		1
k=−1 z drugiej −		<x<−
	6		6

czyli z (2) mamy:

	5		1		1		5
−		<x<−		lub		<x<
	6		6		6		6

============================== Teraz narysuj oś liczbową , zaznacz te przedziały i odczytaj część wspólną:

Walec: Super Pięknie dziękuje <3

Mila: