 Witam. Termin olimpiady "o diamentowy indeks" się skończył, więc zamieszczam rozwiązanie
pierwszego zadania.
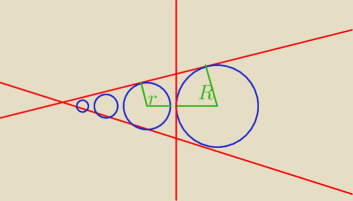
Dane są 2 okręgi, jeden o promieniu r, drugi o promieniu R, trzeba obliczyć
pole trójkąta ograniczonego przez styczne do tych okręgów. r<R.
Oznaczmy jego wysokość przez h.
Witam. Termin olimpiady "o diamentowy indeks" się skończył, więc zamieszczam rozwiązanie
pierwszego zadania.
Dane są 2 okręgi, jeden o promieniu r, drugi o promieniu R, trzeba obliczyć
pole trójkąta ograniczonego przez styczne do tych okręgów. r<R.
Oznaczmy jego wysokość przez h.
| r | ||
Rozważmy ciąg okręgów podobnych, każdy podobny do kolejnego ze skalą | . | |
| R |
| r | r | 1 | 2rR | ||||||||||||||
h = 2r + 2r * | + 2r * ( | )2 + ... = 2r * | = | ||||||||||||||
| R | R |
| R−r |
| r | a | ||
= | ⇒ a=√rR | ||
| a | R |
| 1 | (rR)3/2 | |||
stąd P = | ah = | |||
| 2 | R−r |
| r | a/2 | ||
= | ⇒ a=2√rR | ||
| a/2 | R |
| 2(rR)3/2 | ||
P = | ||
| R−r |
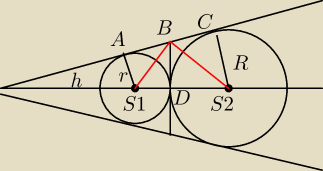 można tak
AB=BC=BD
można tak
AB=BC=BD
| BD | R | ||
= | |||
| r | BD |
| r | R | ||
= | |||
| h−r | h+R |
| 2rR | ||
P= | √rR | |
| R−r |