Wykresy
Krzysiek60: Rozwiaz graficznie
1) |x−1|+|y−1|≤1
2) |x|+|y|= |x−1|+|y−1|
27 paź 10:36
jc: 1) sfera kwadratowa o środku w punkcie (1,1)
2) zbiór punktów równoodalonych od (0,0) i (1,1) w metryce miejskiej.
Na pewno prosta = symetralna odcinka (0,0)(1,1).
27 paź 10:46
Krzysiek60: jc
Nie wiem jak zrobic te wykresy .
Nie mam problemu np z |x−y|<5 czy ale tutaj mam z tym
27 paź 10:50
math: porozbijaj na przypadki żeby pozbyć się wartości bezwzględnych i wtedy; żmudnie ale do
wykonania;
dalej już prosto, trochę podstawień i rysujesz,
daj znać czy pomogło
pzdr
27 paź 12:07
Krzysiek60:
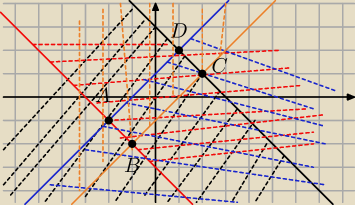
Pierwsze
1) x≥1 i y≥1
x−1+y−1≤1
y≤−x+3
2) x≥1 i y<1
x−1+(1−y)≤1
−y≤1−x ⇒y≥x−1
3) x<1 i y≥1
1−x+y−1≤1
y≤1+x
4) x<1 i y<1
1−x+(1−y)≤1
y≥−x−3
Z rysunku to mi wychodzi taki prostokat ABCD o obszarem wewnatrz lacznie
Za drugi sie wezme jak zrobie porzadki

27 paź 13:31
Krzysiek60: natomiast z drugim mam powazny klopot z wypisaniem tych warunkow
Bo jezeli zaczne je wypisywac to bedzie ich az 24
bo np x≥0 y≥0 x≥1 y≥1
2) x≥0 y≥0 x≥1 y<1 itd
no chyba ze zle ale to niechcialbym robic dalej zle zeby to nie wpadlo wpamiec .
27 paź 15:02
iteRacj@: witaj!
4) x<1 i y<1
1−x+1−y≤1
−x−y≤−1
y≥−x+1 i jest zapowiedziany przez jc kwadrat z wnętrzem (jeśli tak można to nazwać)
27 paź 15:07
27 paź 15:07
Krzysiek60: Dzien dobry

To tak jest jak sie liczy w pamieci

A ten drugi wykres ?
Mozesz wypisac warunki
27 paź 15:10
Pytający:
W pierwszym zadaniu w czwartym przypadku pomyliłeś się, wychodzi y≥−x+1 (a graficznie kwadrat).
W drugim zadaniu przy rozbiciu na przypadki będziesz miał ich 3*3=9, bo są po 3 przedziały do
rozpatrzenia dla iksa i igreka:
x<0
0≤x<1
1≤x
y<0
0≤y<1
1≤y
27 paź 15:10
jc: Znasz rozwiązania nierówności (widzialem)
|x|+|y|≤1
Dodam, że wystarczy rozpatrzyć nieujemne x,y, a potem odbijać symetrycznie rysunek.
Rozwiązaniem jest kwadrat o wierzchołkach (1,0), (0,1), (−1,0), (0, −1).
Nierówność
|x−5|+|y−2|≤1
opisuje wspomniany wcześniej kwadrat odpowiednio przesunięty.
Nowy środek = (5,2)
Nowe wierzchołki = (6,2), ... (sam potrafisz dodać).
27 paź 15:31
Krzysiek60: Niestety nie rozumiem
Chcialem to rozpisac tak
x∊(−∞,0) i y∊(−∞,0)
rownanie ma postac −x−y= 1−x+1−y
teraz x∊<0,1) i y∊<0,1)
x+y= 1−x+1−y
teraz dla x∊<1,∞) i y∊<1,∞)
x+y+x−1+y−1
ale to pewnie nie tak
27 paź 15:33
jc: Czym jest zbiór opisany równaniem
(x−5)2+(y−2)2≤1 ?
To bardzo podobna sytuacja.
27 paź 15:35
Krzysiek60: Kolo o srodku S=(5,2) i r=1
Ale jak to sie ma do zadania nr 2 ?
Probuje to zrozumiec
Bo jesli napiszse
|x|2+|y|2= (|x−1|)2+(|y−1|)2
ti x2+y2= (x−1)2+(y−1)2
skorzystalem z tego ze
|x|2= x2
27 paź 15:42
jc: Krzysiek, lepiej pisz po jednym zadaniu, bo teraz nie wiadomo, z którym masz jeszcze problem,
no i do którego odnoszą się wpisy.
27 paź 15:42
Krzysiek60: jc
Zadanie nr 1 rozumiem iTwoj zapis z tym kolem do tej nierownosci tez .
natomiast mam problem z zadaniem nr 2 z wypisaniem przedzialow
27 paź 15:45
Krzysiek60: Pytajacy pisal ze ma byc ich 9
27 paź 15:46
jc: W drugim zadaniu masz zbiór punktów, których odległość od punktu (0,0)
jest taka sama, jak odległość od punktu (1,1), ale w metryce miejskiej.
Ładniej będzie, kiedy weźmiesz punkty (−1,−1), (1,1).
Potem będziesz mógł przesunąć rozwiązanie (po przeskalowaniu).
Wydaje mi się, że będą to dwie rozsunięte ćwiartki połączone odcinkiem.
27 paź 15:50
jc: Teraz wziąłbym nawet (−1,1) i (1,−1)
Rozwiązaniem jest, jak mi się wydaje suma ćwiartek
x,y ≥ 1
x,y ≤ −1
oraz odcinek
(−1,−1), (1,1).
27 paź 15:54
jc:
|x−1|+|y+1| = |x+1|+|y−1|
Rozwiąznia
x=y
x,y ≥ 1
x,y ≤−1
27 paź 15:59
iteRacj@:
a może to być odcinek (−1,0), (0,−1) ?
27 paź 16:00
Krzysiek60: No jest taki smieszny ten wykres na wolframie .
A zobacz na moj post 15 : 33
wyjdzie mi w 1 i 3 przedziale sprzecznosc a w drugim y=−x−1
27 paź 16:03
iteRacj@:
źle odczytałam wykres: czy może to być odcinek (1,0), (0,1)?
27 paź 16:08
jc: Iteracja, zmieniłem dane, aby łatwiej było rozwiązać zadanie.
27 paź 16:08
jc: W oryginalnym zadaniu to odcinek wspomniany przez iteRację
i dwie ćwiartki
x≤0, y≥1
oraz
x≥1, y≤0
27 paź 16:12
Krzysiek60:
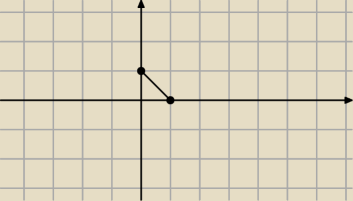
Tylko ze w moim rozwiazaniu bedzie tylko ten odcinek
27 paź 16:12
iteRacj@: OK, a ja uparcie analizuję wykres podanego przez Krzyśka równania
27 paź 16:13
Krzysiek60: Jesli bym mogl prosic o wyjasnienie dlaczego te dwie cwiartki wchodza do rozwiazania ?
27 paź 16:20
jc:
|x|+|y|=|x−1|+|y−1|
x=0, y=2, L=2+0, P=1+1=2
x=−3, y=4, L=3+4=7, P=4+3=7
27 paź 16:21
jc: x≤0, y≥1
|x|+|y|=|x−1|+|y−1|
L=−x+y=y−x
P=−(x−1)+(y−1)=−x+1+y−1=y−x
L=P
Podobnie z drugą ćwiartką.
27 paź 16:23
jc: Krzysiek, pomyśl sobie o dwóch równo rosnących kwadratowych okręgach
o środkach w punktach (0,0) i (1,1).
Na początku będą rozłączne, następnie na moment złączą się wzdłuż odcinka (0,1), (1,0),
a potem będą miały ciągle wspólne fragmenty dwóch dwóch krawędzi.
27 paź 16:27
Krzysiek60: Dobrze . Mysle ze juz lapie . dziekuje Ci .
27 paź 16:36
Mila:
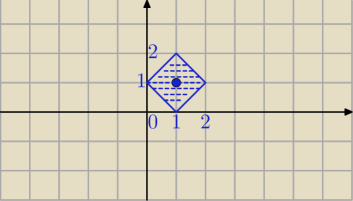
1)
|x−1|+|y−1|≤1
27 paź 17:08
Krzysiek60: Dobry wieczór

A to drugie jakbys rozwiazala
Milu
27 paź 17:11
27 paź 17:16
math: zapomniałem zaproponować, pomyśl o tym jak o przesunięciu

|x|+|y|=1; następnie pomyśl o tym czym jest postać
|x|+|y|≤1 a następnie przesunięcie y i x o jeden w prawo pzdr
27 paź 17:19
Krzysiek60: Mialbym prosbe
czy ktos moze to rozpisac zadanie nr 2 na przedzialach ?
Pytajacy napisal ze przypadkow bedzie 9
27 paź 17:33
Pytający:
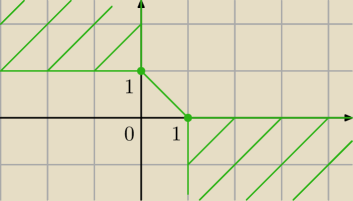
A te przypadki takie by były (acz to nieco siermiężne podejście):
|x|+|y|=|x−1|+|y−1|
• x<0 ∧ y<0 ∧ −x−y=1−x+1−y // brak rozwiązań
• x<0 ∧ 0≤y<1 ∧ −x+y=1−x+1−y // brak rozwiązań
• x<0 ∧ 1≤y ∧ −x+y=1−x+y−1 // x<0 ∧ 1≤y
• 0≤x<1 ∧ y<0 ∧ x−y=1−x+1−y // brak rozwiązań
• 0≤x<1 ∧ 0≤y<1 ∧ x+y=1−x+1−y // 0<x<1 ∧ y=1−x
• 0≤x<1∧ 1≤y ∧ x+y=1−x+y−1 // x=0 ∧ 1≤y
• 1≤x ∧ y<0 ∧ x−y=x−1+1−y // 1≤x ∧ y<0
• 1≤x ∧ 0≤y<1 ∧ x+y=x−1+1−y // 1≤x ∧ y=0
• 1≤x ∧ 1≤y ∧ x+y=x−1+y−1 // brak rozwiązań
27 paź 17:34
Pytający:
O, mówisz masz.

27 paź 17:34
Krzysiek60: Dziekuje pięknie .
To bylo zadanie maturalne .Wiec poplynalem

27 paź 17:40
Mila:
2)
(*) |x|+|y|= |x−1|+|y−1|⇔
a) |y|−|y−1|=|x−1|−|x| i
y≥1
|y|=y, |y−1|=y−1
y−(y−1)=|x−1|−|x|⇔1=|x−1|−|x|
|x−1|−|x|=1
♦x≥1 brak rozwiązań
♦x∊<0,1)
−x+1−x=1
x=0
♦x<0
−x+1+x=1
1=1
równanie (*) jest spełnione przez każdą parę (x,y) taką, że :
(x,y) gdzie :
x≤0 i y≥1
b)|y|−|y−1|=|x−1|−|x| i
y∊<0,1)
|y|=y
|y−1|=−y+1
y−(−y+1)=|x−1|−|x|
2y−1=|x−1|−|x|
♦x≥1
(x,0) i x≥1
♦x∊<0,1)
| | 1 | |
y= |
| *(−x+1−x+1)⇔y=−x+1 ( odcinek ) |
| | 2 | |
♦x<0
| | 1 | | 1 | |
y= |
| (−x+1+x+1)= |
| *2=1∉D |
| | 2 | | 2 | |
c)|y|−|y−1|=|x−1|−|x| i y<0
−y−(−y+1)=|x−1|−|x|
−y+y−1=|x−1|−|x|
−1=|x−1|−|x|
|x−1|−|x|=−1
♦x≥1
x−1−x=−1
−1=−1
pary:
(x,y) gdzie x≥1 i y<0
♦x∊<0,1)
|x−1|−|x|=−1⇔−x+1−x=−1
−2x=−2
x=1∉<0,1)
♦x<0
−x+1−(−x)=−1
−x+1+x=−1
1=−1 sprzeczność
odpowiedź:
{
(x,y) : x≤0 i y≥1 } lub {
(x,y) : y=−x+1 i x∊<0,1>}
lub {
(x,y) gdzie x≥1 i y<0}
Nie wiem, czy czegoś nie zgubiłam

27 paź 18:18
Krzysiek60: Dobrze . Sprawdze Milu

27 paź 18:53
 Pierwsze
1) x≥1 i y≥1
x−1+y−1≤1
y≤−x+3
2) x≥1 i y<1
x−1+(1−y)≤1
−y≤1−x ⇒y≥x−1
3) x<1 i y≥1
1−x+y−1≤1
y≤1+x
4) x<1 i y<1
1−x+(1−y)≤1
y≥−x−3
Z rysunku to mi wychodzi taki prostokat ABCD o obszarem wewnatrz lacznie
Za drugi sie wezme jak zrobie porzadki
Pierwsze
1) x≥1 i y≥1
x−1+y−1≤1
y≤−x+3
2) x≥1 i y<1
x−1+(1−y)≤1
−y≤1−x ⇒y≥x−1
3) x<1 i y≥1
1−x+y−1≤1
y≤1+x
4) x<1 i y<1
1−x+(1−y)≤1
y≥−x−3
Z rysunku to mi wychodzi taki prostokat ABCD o obszarem wewnatrz lacznie
Za drugi sie wezme jak zrobie porzadki 
 To tak jest jak sie liczy w pamieci
To tak jest jak sie liczy w pamieci A ten drugi wykres ?
Mozesz wypisac warunki
A ten drugi wykres ?
Mozesz wypisac warunki
 Tylko ze w moim rozwiazaniu bedzie tylko ten odcinek
Tylko ze w moim rozwiazaniu bedzie tylko ten odcinek
 1)
|x−1|+|y−1|≤1
1)
|x−1|+|y−1|≤1
 A to drugie jakbys rozwiazala Milu
A to drugie jakbys rozwiazala Milu
 |x|+|y|=1; następnie pomyśl o tym czym jest postać
|x|+|y|≤1 a następnie przesunięcie y i x o jeden w prawo pzdr
|x|+|y|=1; następnie pomyśl o tym czym jest postać
|x|+|y|≤1 a następnie przesunięcie y i x o jeden w prawo pzdr
 A te przypadki takie by były (acz to nieco siermiężne podejście):
|x|+|y|=|x−1|+|y−1|
• x<0 ∧ y<0 ∧ −x−y=1−x+1−y // brak rozwiązań
• x<0 ∧ 0≤y<1 ∧ −x+y=1−x+1−y // brak rozwiązań
• x<0 ∧ 1≤y ∧ −x+y=1−x+y−1 // x<0 ∧ 1≤y
• 0≤x<1 ∧ y<0 ∧ x−y=1−x+1−y // brak rozwiązań
• 0≤x<1 ∧ 0≤y<1 ∧ x+y=1−x+1−y // 0<x<1 ∧ y=1−x
• 0≤x<1∧ 1≤y ∧ x+y=1−x+y−1 // x=0 ∧ 1≤y
• 1≤x ∧ y<0 ∧ x−y=x−1+1−y // 1≤x ∧ y<0
• 1≤x ∧ 0≤y<1 ∧ x+y=x−1+1−y // 1≤x ∧ y=0
• 1≤x ∧ 1≤y ∧ x+y=x−1+y−1 // brak rozwiązań
A te przypadki takie by były (acz to nieco siermiężne podejście):
|x|+|y|=|x−1|+|y−1|
• x<0 ∧ y<0 ∧ −x−y=1−x+1−y // brak rozwiązań
• x<0 ∧ 0≤y<1 ∧ −x+y=1−x+1−y // brak rozwiązań
• x<0 ∧ 1≤y ∧ −x+y=1−x+y−1 // x<0 ∧ 1≤y
• 0≤x<1 ∧ y<0 ∧ x−y=1−x+1−y // brak rozwiązań
• 0≤x<1 ∧ 0≤y<1 ∧ x+y=1−x+1−y // 0<x<1 ∧ y=1−x
• 0≤x<1∧ 1≤y ∧ x+y=1−x+y−1 // x=0 ∧ 1≤y
• 1≤x ∧ y<0 ∧ x−y=x−1+1−y // 1≤x ∧ y<0
• 1≤x ∧ 0≤y<1 ∧ x+y=x−1+1−y // 1≤x ∧ y=0
• 1≤x ∧ 1≤y ∧ x+y=x−1+y−1 // brak rozwiązań


 2)
(*) |x|+|y|= |x−1|+|y−1|⇔
a) |y|−|y−1|=|x−1|−|x| i y≥1
|y|=y, |y−1|=y−1
y−(y−1)=|x−1|−|x|⇔1=|x−1|−|x|
|x−1|−|x|=1
♦x≥1 brak rozwiązań
♦x∊<0,1)
−x+1−x=1
x=0
♦x<0
−x+1+x=1
1=1
równanie (*) jest spełnione przez każdą parę (x,y) taką, że :
(x,y) gdzie : x≤0 i y≥1
b)|y|−|y−1|=|x−1|−|x| i y∊<0,1)
|y|=y
|y−1|=−y+1
y−(−y+1)=|x−1|−|x|
2y−1=|x−1|−|x|
2)
(*) |x|+|y|= |x−1|+|y−1|⇔
a) |y|−|y−1|=|x−1|−|x| i y≥1
|y|=y, |y−1|=y−1
y−(y−1)=|x−1|−|x|⇔1=|x−1|−|x|
|x−1|−|x|=1
♦x≥1 brak rozwiązań
♦x∊<0,1)
−x+1−x=1
x=0
♦x<0
−x+1+x=1
1=1
równanie (*) jest spełnione przez każdą parę (x,y) taką, że :
(x,y) gdzie : x≤0 i y≥1
b)|y|−|y−1|=|x−1|−|x| i y∊<0,1)
|y|=y
|y−1|=−y+1
y−(−y+1)=|x−1|−|x|
2y−1=|x−1|−|x|

