Okresl w zaleznosci od a liczność klasy równoważności [a].
asdf: Dane jest odwzorowanie f: R→R takie że x
3−3x+2.
Niech S = (R, grS, R) będzie relacją taką, że S = { (x, y) : f(x) = f(y) }
Niech a ∊ R. Okresl w zaleznosci od a liczność klasy równoważności [a].
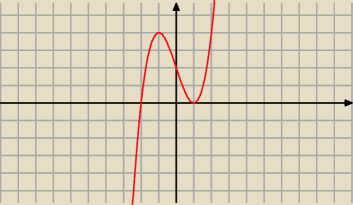
Tu jest wykres
https://imgur.com/a/DRmxqlv
Jak to zbadać, nie za bardzo rozumiem, prosze o wyjasnienie
26 paź 22:13
Adamm:
"Niech S = (R, grS, R)"
co to znaczy
26 paź 22:28
asdf: To chyba określenie relacji, że działa z R na R
Takie oznaczenia mam w większości zestawów
26 paź 22:33
26 paź 23:42
PW: Widzę, że już dostał. Publiczność nawet nie wie za co.
26 paź 23:49
Mila:
Ważne, że my wiemy

Pozdrawiam

26 paź 23:51
PW: Dziękuję

26 paź 23:53
asdf: Tak, wzięte stamtąd
No więc, wie ktoś jak to zrobić?

27 paź 11:30
Adamm:
czyli jak rozumiem, relacja jest określona bardzo dziwnie
grS tak naprawdę to nasza relacja
S to trójka złożona ze zbioru A, relacji, i zbioru B
relacja jest określona na AxB
27 paź 11:42
Adamm:
[a] = {x: f(x)=f(a)}
a∊(−
∞, −2)∪(2,
∞)
| [a] | = 1
a∊{−2, −1, 1, 2}
| [a] | = 2
a∊(−2, −1)∪(−1, 1)∪(1, 2)
| [a] | = 3
27 paź 11:53
asdf: Hmmm, a skąd się biorą te liczności zbioru?
Kojarze podobne zadania typu: "zbadaj ilość rozwiązań rownania w zaleznosci od parametru m" i
tam sie brało proste rownolegle do osi OX
Tu jest tak samo?
27 paź 12:13
Adamm:
patrzysz na to co dostajesz jak podstawisz f(a)
klasy abstrakcji będą się składały z przecięcia się prostej y=f(a) oraz funkcji y=x3−3x+2
27 paź 12:31
asdf: Rozumiem!
Wielkie dzięki
27 paź 12:41
math: no nie bardzo widzę jak szukasz analogii ale...
mamy: [ garść faktów ]
f(x) = x
3−3x+2 zdefiniowaną na f: R →R; jest to wielomian więc mamy bijekcję;
mamy zdefiniowaną relację:
{ (x, y) : f(x) = f(y) } − gdzie f jest zdefiniowana wyżej;
no więc sprawdzamy z jakimi klasami równoważności mamy tutaj do czynienia:
#1 wyznacz sobie możliwe klasy abstrakcji − zrób partycje:
co wyróżnia dane klasy abstrakcji
jak już to zrobisz, znajdziesz je to wtedy bierzesz się za liczności

czyli analizujemy co my tu mamy, jak łatwo zauważyć, co badamy?
czytamy relację:
dwa elementy ze zbioru R są w relacji gdy ich wartości są równe:
relację oznaczę tutaj roboczo ∼
tzn dowolne x,y∊R (x∼y) wtedy i tylko wtedy gdy f(x)=f(y)
no to już powinno być jasne, czyli jeśli dwa argumenty osiągają tę samą wartość to są ze sobą w
relacji
czyli łopatologiczne, możemy wziąć linijkę i sprawdzać; przyjmijmy kierunek od dołu w górę,
i tak lecimy i widzimy że na przedziale od
−
∞ do −2 wartości są pojedyńcze, tzn dla dowolnego x z tego przedziału,
jest jednoznacznie przypisana wartość.
kolejno na wysokości y = 0 [ inaczej f(x) = 0 ] mamy przyjętą wartość dwukrotnie;
kolejno idąc w górę z naszą linijką dane wartości są przyjmowane aż dla 3 argumentów aż do
mometnu
gdy dojdziemy na poziom y = 4
i później znowu wartości są przyjmowane dla pojedynczych argumentów x; jasne?
i teraz zbieramy przeanalizowane informację w zbiory żeby nie rozbijać na zbyt wiele przypadków
co zrobił
kolega wyżej.
clean&clear?
jak są jeszcze pytania czy wątpliwości to pisz
pzdr
27 paź 12:49
asdf: clean and clear

aczkolwiek z tych relacji kuleje strasznie

27 paź 18:04
 Pozdrawiam
Pozdrawiam


 [a] = {x: f(x)=f(a)}
a∊(−∞, −2)∪(2, ∞)
| [a] | = 1
a∊{−2, −1, 1, 2}
| [a] | = 2
a∊(−2, −1)∪(−1, 1)∪(1, 2)
| [a] | = 3
[a] = {x: f(x)=f(a)}
a∊(−∞, −2)∪(2, ∞)
| [a] | = 1
a∊{−2, −1, 1, 2}
| [a] | = 2
a∊(−2, −1)∪(−1, 1)∪(1, 2)
| [a] | = 3
 czyli analizujemy co my tu mamy, jak łatwo zauważyć, co badamy?
czytamy relację:
dwa elementy ze zbioru R są w relacji gdy ich wartości są równe:
relację oznaczę tutaj roboczo ∼
tzn dowolne x,y∊R (x∼y) wtedy i tylko wtedy gdy f(x)=f(y)
no to już powinno być jasne, czyli jeśli dwa argumenty osiągają tę samą wartość to są ze sobą w
relacji
czyli łopatologiczne, możemy wziąć linijkę i sprawdzać; przyjmijmy kierunek od dołu w górę,
i tak lecimy i widzimy że na przedziale od
−∞ do −2 wartości są pojedyńcze, tzn dla dowolnego x z tego przedziału,
jest jednoznacznie przypisana wartość.
kolejno na wysokości y = 0 [ inaczej f(x) = 0 ] mamy przyjętą wartość dwukrotnie;
kolejno idąc w górę z naszą linijką dane wartości są przyjmowane aż dla 3 argumentów aż do
mometnu
gdy dojdziemy na poziom y = 4
i później znowu wartości są przyjmowane dla pojedynczych argumentów x; jasne?
i teraz zbieramy przeanalizowane informację w zbiory żeby nie rozbijać na zbyt wiele przypadków
co zrobił
kolega wyżej.
clean&clear?
jak są jeszcze pytania czy wątpliwości to pisz
pzdr
czyli analizujemy co my tu mamy, jak łatwo zauważyć, co badamy?
czytamy relację:
dwa elementy ze zbioru R są w relacji gdy ich wartości są równe:
relację oznaczę tutaj roboczo ∼
tzn dowolne x,y∊R (x∼y) wtedy i tylko wtedy gdy f(x)=f(y)
no to już powinno być jasne, czyli jeśli dwa argumenty osiągają tę samą wartość to są ze sobą w
relacji
czyli łopatologiczne, możemy wziąć linijkę i sprawdzać; przyjmijmy kierunek od dołu w górę,
i tak lecimy i widzimy że na przedziale od
−∞ do −2 wartości są pojedyńcze, tzn dla dowolnego x z tego przedziału,
jest jednoznacznie przypisana wartość.
kolejno na wysokości y = 0 [ inaczej f(x) = 0 ] mamy przyjętą wartość dwukrotnie;
kolejno idąc w górę z naszą linijką dane wartości są przyjmowane aż dla 3 argumentów aż do
mometnu
gdy dojdziemy na poziom y = 4
i później znowu wartości są przyjmowane dla pojedynczych argumentów x; jasne?
i teraz zbieramy przeanalizowane informację w zbiory żeby nie rozbijać na zbyt wiele przypadków
co zrobił
kolega wyżej.
clean&clear?
jak są jeszcze pytania czy wątpliwości to pisz
pzdr
 aczkolwiek z tych relacji kuleje strasznie
aczkolwiek z tych relacji kuleje strasznie 