uklady rownan REX: Oblicz pole trójkąta ograniczonego prostą y=1/2x+3 i wykresem funkcji f: a. f(x) =w klamerce : 1 dla xe ( − nieskonczonosc,−2> x+3 dla xe (−2,nieskonczonosc ) b. f(x) = w klamerce : −x dla xe ( − nieskonczonosc , 1> 2x−3 dla xe (1, nieskonczonosc )

Krzysiek60: Zrob najpierw wykres

REX: Nie umiem... błagam o pomoc

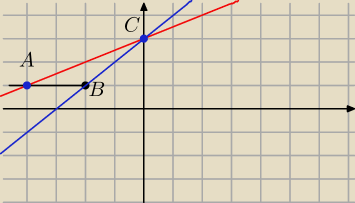
Krzysiek60: Z rysunku (do a)

	1
P=		a*h
	2

a=2 h=2 podsatw i policz

REX: Ale co mam pod co podstawić ? Nie rozumiem

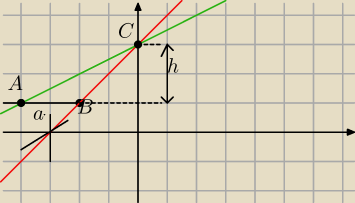
Krzysiek60: Czarny to y=1 dla x∊(−∞,−2> czerowny to y=x+3 dla x∊(−2,∞)

	1
zielony to y=		x+3
	2

Te pierwszs edwie rysujesz w tych przedzialach co podane proste te ograniczaja trojkat ABC AB to podstawa −a h to wysokosc tego trojkata Z rysunku odczytujesz AB=2 i h=2 podstaw do wzoru z 19 :06 i policz to pole Zrob tak samo rysunek do przykladu b) Wykres funkcji liniowej powinienes umiec narysowac

REX: Niestety nie rozumiem jak to jest zrobione , w sensie ten wykres ,skad te proste powstaly zielona i czerwona.

Jolanta:

	1
umiesz narysować wykres y=		x+3
	2

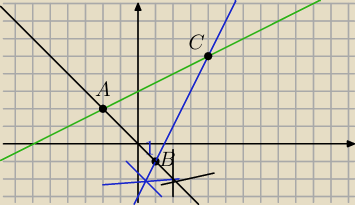
Krzysiek60: b) f(x) narysujemy najpierw f(x)={ −x dla x∊(−∞,1> {2x−3 dla (1,∞) czarna to f(x)−−x ale tylko do x=1 niebieski to f(x)= 2x−3 ale tylko ta czesc od x=1 do gory (do nieskonczonosci

	1
Teraz rysujemy prosta y=		x+3 zielona
	2

Widzisz ze te proste ograniczaja trojkat ABC Pole trojkata (wzorow do wyboru do koloru

Krzysiek60: Wyznaczamy wspolrzedne punktu A czyli wykres zielony i czarny {y=−x

	1
{y=		x+3
	2

	1
−x=		x+3 (mnoze przez 2
	2

−2x=x+6 −3x=6 x=−2 y=−x y=−(−2)=2 Punkt A=(−2,2) lub odczytac z rysunku WYznaczam wspolrzedne punktu B Wykres czarny i niebieski {y=−x {y=2x−3 −x= 2x−3 −3x=−3 x=1 y=−x y=−1 Punkt B=(1,−1) lub odcztac z rysunku Wyznaczam wspolrzedne punktu C wykres zielony i niebieski

	1
{y=		x+3
	2

{y=2x−3

1
	x+3= 2x−3 (mnoze przez 2
2

x+6=4x−6 −3x=−12 x=4 podstawiam x do rownania y=2x−3 to y=2*4−3=5 Punkt C =(4,5) Masz juz wszystko do policzenia pola |AB| dlugosc podstawy (oznaczmy a przez a (jest na to wzor |AB|= √(1−(−2)²+(−1−2)² = √18 = 3√2 =a Piszemy rownanie prostej AB mamy bo to y=−x (kierumkowa posatc wiec ogolna jest x+y=0 Odleglosc punktu C od prostej AB to wysokosc trojkata (h) jest na to wzor wspolrzedne punktu C=(4,5) gdzie x₀=4 i y₀=5 mamy x+y=0 wiec A=1 B=1 C=0

	|1*4+1*5+0|		9
h=		=
	√12+12		√2

	1
P=		*a*h
	2

	1		9		1
P=		*3√2*		= 13		[j2]
	2		√2		2

To byl najdluszy sposob .