wartosc Krzysiek60: Znajdz najmniesza i najwieksza wartosc parametru z dla ktorych spelniony jest uklad warunkow 2x+y≥2 i x+3y≥3 i x−y≥−1 i 3x−y≤6 i x+y≤5 i z=x+2y przez conajmniej jedna pare liczb rzeczywistych x,y.

	11
Odp zmax=8 zmin=
	5

czy tutaj nalezy rysowac wykresy ?

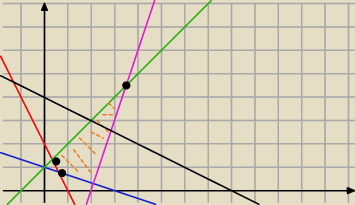
Blee: dokładnie zakreskowany jest obszar będący rozwiązaniami czterech nierówności jako, że z = x + 2y można zapisać jako: y = −x/2 + z/2 czyli będziesz miał funkcję malejącą to masz trzy punkty podejrzane oto, że przez nie będą przechodziły funkcje 'maksymalna' i 'minimalna' wyznaczasz współrzędne tych punktów i wyznaczasz 'z' ... tylko z_max = 8 mi tutaj nie pasuje (patrz czarna prosta)

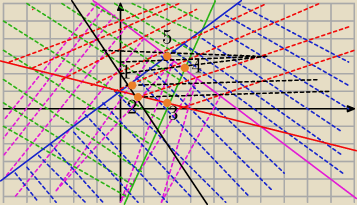
Krzysiek60: czarna y= −x+2

	1
czerwona y=−		x+1
	3

niebieska y= 1+x zielona y= 3x−6 rozowa y=−x+5 mam obszar ograniczony przez te 5 punktow czarna z niebieska (nr 1 x=0,5 i y= 1,5 czarna z czerwona (nr 2

	3		4
x=		i y=
	5		5

czerwona i zielona x=2,1 y=0,3 rozowa i zielona (nr 4

	11		1
x=		y= 2
	4		4

rozowa i niebieska )(nr 5 x=2 i y=3 z= x+2y z_max bedzie dla x=2 iy=3 z_max= 2+2*3=8 Teraz min z= 0,5*2*1,5= 3,5 z= 2,1+2*0,3= 2,7

	3		4		11
z=		+2*		=		tutaj bedzie min
	5		5		5

ostatniego nie sprawdzam bo jest wiekszse tak mi wyszlo czyli bedzie to punkt nr 5 i punkt nr 2 .rzucisz okiem ? Punkty przeciecia sie prostych sprawdzalem dwa razy wiec powinny byc OK.

Blee: Krzysiek ... z tego co narysowałeś NIC nie widać

Blee: ach ... zapomniałem o x+y ≤ 5 ... to wiele wyjaśnia

Krzysiek60: taki rysunek wyszedl . Najlepiej bylo narysowac potem drugi tylko z tym prawdziwym obszarem