liczby zespolone
Dominik: Znaleźć miejsca geometryczne
|z| < 4
√22 + 02 <4
p{4] < 4
2<4

i co dalej?
25 paź 13:31
Adamm:
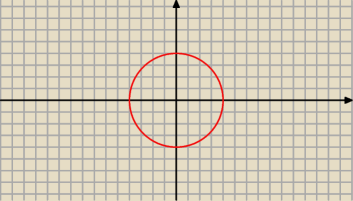
25 paź 13:33
Dominik: Ale ten mój tok myślenia z tym równaniem jest ok? i dlaczego środkiem jest 0?
25 paź 13:40
Jerzy:
|z| < 4 ⇔ |z − 0| < 4 .... wnętrze koła o śroku S(0,0) i promieniu r = 4
25 paź 13:44
Dominik: A dlaczego w module jest wpisane z−0?
25 paź 13:47
Adamm:
bo jak przesuwasz o wektor z0, to dostajesz |z−z0|<4
Jerzy chciał zaznaczyć, że nie przesuwamy tego koła
25 paź 13:50
Jerzy:
Bo: z = z − 0 , a zapis: |z − z0| < a , oznacza zbiór punktów płaczyzny zespolonej,których
odległość od punktu z0 jest mniejsza od a.
25 paź 13:50
Dominik: a czasem nie jest tak, że z=x+iy

25 paź 13:58
Dominik: Nie rozumiem skąd tam jest z−0 i jaką wartość przyjmuje z źe wychodzi 0. W takim razie z musi
być równe 0.. Ale jak?
25 paź 13:59
Jerzy:
Jest tak, z = x + iy
25 paź 13:59
Jerzy:
Jeszcze raz. Popatrz post 13:50. Jeśli z0 = 0 , to : |z − z0| = |z − 0| = |z|
25 paź 14:01
Jerzy:
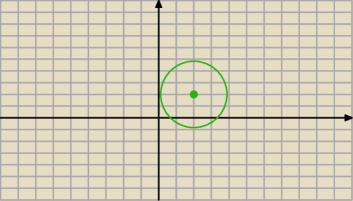
Tutaj masz przykład: |z − z
0| = 2 , gdzie: z
0 = 2 + 2i , czyli: |z − (2 + 2i)| = 2
25 paź 14:04
Dominik: ale to jest jakaś reguła, że z = 0? Nie rozumiem tego

25 paź 14:08
Jerzy:
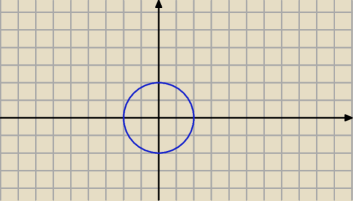
Popatrz na rysunek 14:04 , gdzie z
0 = 2 + 2i. Gdyby z
0 = 0 , to mielibyśmy:
|z − z
0| = 2 ⇔ |z − 0| = 2 ⇔ |z| =2 ( i patrz rysunek)
25 paź 14:11
Pytający:
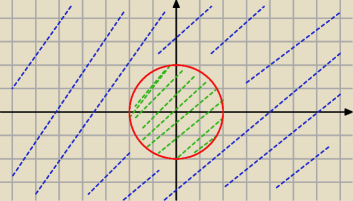
Ja tylko dorzucę taki rysunek.
|
z|=2
|
z|<2
|
z|<2
25 paź 14:13
Pytający:
Poprawka do ostatniej linijki:
|z|>2
25 paź 14:14
Dominik: A możesz mi na tym przykładzie wytłumaczyć? Może załapię..
| z−3+4i |<5
25 paź 14:15
Jerzy:
Autor nie do końca rozumie, co oznacza zapis: |z − z0| = r
25 paź 14:16
Jerzy:
|z − (3 − 4i)| < 5 .... wnętrze okregu o środku S(3 ; −4) i promieniu r = 5
25 paź 14:19
Jerzy:
Tutaj masz: z0 = 3 − 4i
25 paź 14:19
Dominik: No to taki przykład:
|z| < 2 i 0 <φ12π
To będzie wnętrze okręgu o środku (0,0) i r=2 a dalej?
25 paź 14:30
Jerzy:
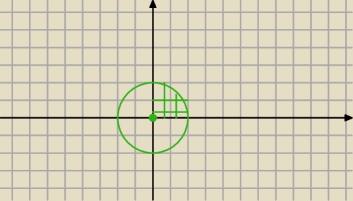
Zakreskowana ćwiartka wnętrza koła S(0,0) i r = 2
25 paź 14:33
Dominik: To dlatego, że π2 = 90 stopni?
25 paź 14:37
Jerzy:
Tak , liczby z tej ćwiartki maja argument główny z zakresu (0;900)
25 paź 14:39
Dominik:
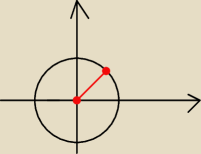
To teraz takie zadanko. Znaleźć miejsce geometryczne punktów, których moduł = 3
| | π | |
|z|=3 i 0= |
| Czyli środek 0, promień 3 a zakres to ta linia wyznaczająca 45 stopni? |
| | 4 | |
25 paź 14:47
Jerzy:
Nie. |z| = 3 , to tylko punkty okręgu S(0,0) i r = 3 , a na tym okręgu jest tylko jeden
punkt,którego argument główny wynosi 450 ( czerwona kropka na twoim okręgu).
25 paź 14:51
Dominik:
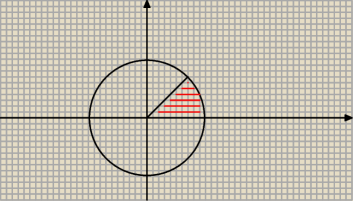
a gdyby było
|z|<3 to by wyglądało tak?
25 paź 14:57
Jerzy:
Też nie. Jeśli: |z| < 3 i α = 450 , to wtedy Twój odcinek (14:47) , ale bez punktu na okręgu.
To co narysowałeś teraz, to: |z| < 10 i 0 < α < 460
25 paź 15:00
Dominik: A dobra łapię. Tzn (14:57) Narysowałem większe żeby było lepiej widać, natomiast r=3 w tym
rysunku
25 paź 15:04
Jerzy:
Narysuj: |z + i| = 1 i α = π
25 paź 15:06
Dominik:
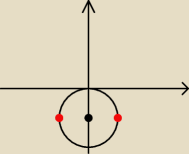
S= (0,−1) i r=1 i a=180
o więc tylko te dwie czerwone kropki?
25 paź 15:17
Dominik: Czy cały ta górna połowa koła w sensie ten łuk?
25 paź 15:18
Jerzy:
Nie. Tylko lewy czerwony punkt, bo leży na okregu (0,−1) i r = 1
i jego argument główny to : α = π
( prawy czerwony punkt ma argument : α = 0 )
25 paź 15:21
Dominik: A rozumiem, żeby to co narysowałem było prawdą, to musiałby być taki warunek a=0 ∧ a=π
25 paź 15:27
Jerzy:
α = 0 lub α = π
25 paź 15:36
Dominik: czemu lub a nie i ?
25 paź 15:48
Jerzy:
Nie ma kąta, który jednocześnie ma miarę 00 i 1800
25 paź 15:52
Dominik: ok, jasne

Dziękuję bardzo
25 paź 16:13
 i co dalej?
i co dalej?


 Tutaj masz przykład: |z − z0| = 2 , gdzie: z0 = 2 + 2i , czyli: |z − (2 + 2i)| = 2
Tutaj masz przykład: |z − z0| = 2 , gdzie: z0 = 2 + 2i , czyli: |z − (2 + 2i)| = 2

 Popatrz na rysunek 14:04 , gdzie z0 = 2 + 2i. Gdyby z0 = 0 , to mielibyśmy:
|z − z0| = 2 ⇔ |z − 0| = 2 ⇔ |z| =2 ( i patrz rysunek)
Popatrz na rysunek 14:04 , gdzie z0 = 2 + 2i. Gdyby z0 = 0 , to mielibyśmy:
|z − z0| = 2 ⇔ |z − 0| = 2 ⇔ |z| =2 ( i patrz rysunek)
 Ja tylko dorzucę taki rysunek.
|z|=2
|z|<2
|z|<2
Ja tylko dorzucę taki rysunek.
|z|=2
|z|<2
|z|<2
 Zakreskowana ćwiartka wnętrza koła S(0,0) i r = 2
Zakreskowana ćwiartka wnętrza koła S(0,0) i r = 2
 To teraz takie zadanko. Znaleźć miejsce geometryczne punktów, których moduł = 3
To teraz takie zadanko. Znaleźć miejsce geometryczne punktów, których moduł = 3
 a gdyby było
|z|<3 to by wyglądało tak?
a gdyby było
|z|<3 to by wyglądało tak?
 S= (0,−1) i r=1 i a=180o więc tylko te dwie czerwone kropki?
S= (0,−1) i r=1 i a=180o więc tylko te dwie czerwone kropki?
 Dziękuję bardzo
Dziękuję bardzo