trójkąt
matura : W trójkącie prostokątnym ABC dane są długości
przeciwprostokątnej |BC|=a i dwusiecznej |AD|=d
Należy wyznaczyć pole trójkąta ABC
Pomoże ktoś?
24 paź 22:54
Mila:
Masz odpowiedź do zadania?
24 paź 23:41
Eta: Hej
Mila 
Mnie wyszło
a Tobie?
24 paź 23:46
Mila:
Dobry wieczór
Eta
Mam identyczny wynik.
Wpisuj swoje.
24 paź 23:48
Eta:
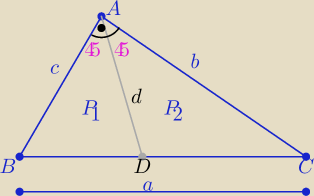
| | bc√2 | |
W trójkącie prostokątnym d= |
| ( możesz to sobie łatwo wykazać |
| | b+c | |
| | 2b2c2 | | 2b2c2 | |
to d2= |
| = |
| |
| | b2+c2+2bc | | a2+2bc | |
2P=bc to 4P
2=b
2c
2 i 2bc=4P
8P
2−4d
2P−a
2d
2=0
Δ
P= 16d
4+32d
2a
2 = 16d
2(d
2+2a
2} ,
√ΔP= 4d
√d2+2a2 a>d
======================
24 paź 23:59
Eta:
Ładne zadanko

24 paź 23:59
Mila:
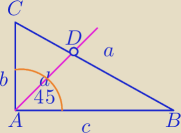
b
2+c
2=a
2
1) Z wzoru na dł. odcinka dwusiecznej
b*c=P, P>0
d
2*a
2+2d
2P=2P
2
2P
2−2d
2 P−a
2d
2=0
Δ=4d
4+8a
2d
2=4d
2*(d
2+2a
2)
| | 2d2+2d√d2+2a2 | | d2+d√d2+2a2 | |
P= |
| = |
| |
| | 4 | | 2 | |
===========================
Mam jeszcze drugi sposób, ale to jutro
Dobranoc

25 paź 00:03
Mila:
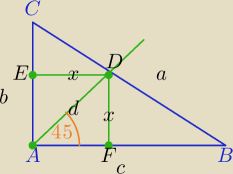
a
2=b
2+c
2
=============
| | EC | | x | | b−x | | x | |
2)ΔCED∼ΔDFB⇔ |
| = |
| ⇔ |
| = |
| |
| | x | | FB | | x | | c−x | |
x
2=(b−x)*(c−x)⇔
bc=x*(b+c) /
2
(bc)
2=x
2*(b
2+2bc+c
2)
bc=P
2P
2=2d
2*P+a
2*p
2
dalej jw.
===========
25 paź 19:04
Mila:
Poprawa zapisu:
2P2=2d2*P+a2d2
25 paź 19:06
 Mnie wyszło
Mnie wyszło
 Mam identyczny wynik.
Wpisuj swoje.
Mam identyczny wynik.
Wpisuj swoje.




