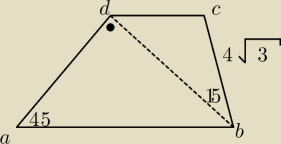
wielokąty na płaszczyźnie wielokąt: Sprawdź, czy czworokąt ABCD o danych przedstawionych na rysunku jest trapezem. Jeśli tak, to oblicz jego pole. a)

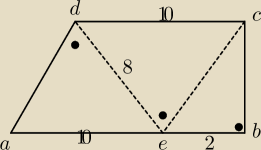
wielokąt: a tu podpunkt b)

wielokąt: Te kropki to kąty proste.

PW: a) Z danych na rysunku nie wynika równoległość ab i cd, to tylko sugestywne wykonanie rysunku. Wystarczy wziąć większy trójkąr abd z doklejonym na zewnątrz odcinkiem bc o długości 4√3, pod tym samym kątem do boku bd.. Nachylenie cd do ab będzie oczywiście inne.

wielokąt: Właśnie w odpowiedziach mam, że w a) czworokąt jest trapezem. Natomiast w b) nie.

ite: b/ z ΔDAE prostokątnego |DA|=6 z ΔDCE prostokątnego |CE|=6 ΔDAE∼ΔDCE (bbb) → |<AED|=|<EDC| |<AEC|=|<AED|+90^o |<ADC|=|<ADE|+90^o → |<ADC|=|<AEC| |AE|=|DC i |DA|=|CE| czworokat AECD jest równoległobokiem → czworokąt ABCD jest trapezem

wielokąt: Rozumiem, dziękuję. A podpunkt a)?

ite: już PW napisał

wielokąt: Według moich odpowiedzi jego odpowiedź jest błędna, gdyż czworokąt ten jest trapezem.

iteRacj@: b/ Podtrzymuję to, co napisałam 16:45, ale teraz zauważyłam, że jeśli <EBC jest prosty, to z pozostałych danych wynika, że EB nie może mieć długości 2. Kąt prosty i taka długość tego odcinka się wzajemnie wykluczają. Może o to chodzi w odpowiedziach (taki trapez nie istnieje).