wielokąty na płaszczyźnie wielokąt: Nierównoległe boki AD i BC trapezu ABCD zawierają się w prostych prostopadłych. Wiedząc, że |AD|=|DC|=8 oraz |<ABC|=30^o, oblicz pole i obwód tego trapezu.

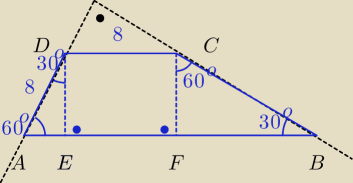
ite: |CF|=|DE|, |EF|=|AD|=|DC|=8 |<ABC|= |<ADE|=30^o |<BAD|= |<FCB|=60^o w ΔADE:

	1
|AE|=		*8=4
	2

	√3
|DE|=		*8=4√3
	2

w ΔCFB:

	1		1
|CF|=		*|CB| → 4√3=		*|CB| → |CB|=8√3
	2		2

	√3		√3
|FB|=		*|CB| → |FB|=		*8√3=12
	2		2

|AB|=12+8+4=24

	1
PABCD=		*(24+8)*4√3
	2

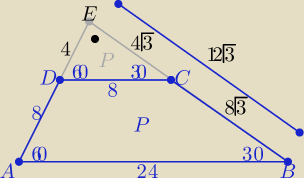Eta: [2 sposób]] Z trójkątów "ekierek" o kątach ostrych 30^o,60^o −−− oznaczenia jak na rys.

	1		1
P= P(ABE)−P(DCE) =		*12*12√3−		*4*4√3
	2		2

P= 64√3 [j²] =========