Trojkat prostokątny podzielony na trzy części #62;:C: Hej! Czy ktoś umie rozwiązać takie zadanie? W trójkącie prostokątnym rownoramiennym przez wierzchołek kąta prostego poprowadzono dwie proste, które podzieliły ten kąt na trzy równe kąty. Wyznacz dlugosci odcinków, na które te proste dzielą przeciwprostokatna o dlugosci c.

Blee: Tak ... jest ktoś kto umie rozwiązać takie zadanie Zadowolna/−y z mojej odpowiedzi? To dobrze

#62;:C: Nie. Udowodnij, że jest taki ktoś, to może będę.

Blee: A pfff ... udowodniłem rozwiązując to zadanie i pokazując je osobom trzecim, które są w stanie pod przysięgą zeznać iż wykonałem to zadanie

Blee: tw. Cosinusów poznałaś/−eś

#62;:C: No domyślam się że tam powinien być zastosowany ten wzór tylko problem w tym, że chyba przeoczam coś oczywistego,bo wydaje mi się, że troche za duzo tych niewiadomych... Jedyne co widzę to że oba ramiona są równe c{2}/2 I po przedzieleniu tymi prostymi tworzą się dwa identyczne rozwartokatne trojkaty i jeden rownoramienny...Można byłoby rozwiązać na podstawie tablicy wartości trygonometrycznych ale sądzę że nie o to chodzi w tym zadaniu :c

#62;:C: Pomoże ktoś?

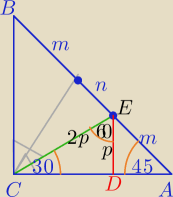
Mila: 1) 2m+n=c

	c
|AC|=
	√2

ΔEDA− Δprostokątny równoramienny |AD|=p 2) WΔCDE: (90,30,60) |CD|=p*√3

	c
p*√3+p=
	√2

	c
p*(1+√3)=		/* (√3−1)
	√2

	c*(√3−1)
p*(3−1)=
	√2

	c*(√3−1)
p=
	2√2

3) W ΔEDA:

	(√3−1)
m=p*√2 ⇔m=c*
	2

	(√3−1)
n=c−2*c*
	2

n=c*(2−√3) =============

	c*(√3−1)
m=
	2

n=c*(2−√3) =========== Posprawdzaj rachunki.

Maciess: Wyniki jak u mnie, więc rachunki raczej w porządku.

Mila:

Eta: 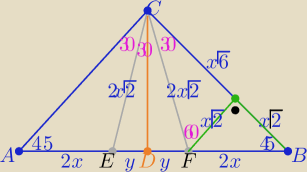2 sposób z trójkątów "ekierek" dane na rys. .............. i z tw. o dwusiecznej w ΔEBC

2x		x√2(√3+1)
	=		⇒ 2x=y(√3+1)
2y		2x√2

podział przeciwprostokątnej : 2x:2y:2x ⇒ (√3+1) :2 : (√3+1) ================

#62;:C: Dziękuję Wam bardzo. Mila, Eta, jesteście niezastąpione. Już wiem gdzie robiłam błąd wczesniej. Rozwiazywalam to twierdzeniem sinusow i wychodziło mi dzielenie przez sin105, a nie wiedziałam, że da się to obliczyć jako sin(a+b) czyli sin(60+45)