zadanie z parametrem asia: Wyznacz wartości parametru m, dla których funkcja f określona wzorem f(x)= (m²−4)x²−4x+1 przyjmuje tylko wartości ujemne.

asia: proszę o jakieś ładne wyjaśnienie

on: aby funkcja f przyjmowala tylko wartosci ujemne to jej wspolczynnik przy x² powinien byc mniejszy od 0, poniewaz mowi to nam, ze ramiona paraboli na wykresie lecą w dół powiedziane jest rowniez, ze TYLKO wartosci ujemne czyli 0 nie bierzemy pod uwage, zatem musimy napisac, ze delta powinna byc mniejsza od 0, poniewaz mowi to nam o braku stycznosci paraboli z osią x

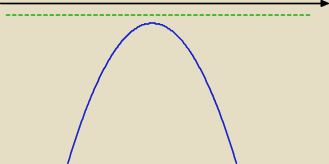
iteRacj@: (dodam jeszcze jedną możliwość do poprzedniego wpisu) 1/ m²−4=0 sprawdzasz, jak położony jest wykres otrzymanej funkcji liniowej (jeśli tak jak zielona prosta to jest to rozwiązanie) 2/ m²−4≠0 sprawdzasz, czy można dobrać tak wartość parametru m, żeby wykres otrzymanej funkcji kwadratowej był położony tak jak na rysunku

on: zatem obliczasz m²−4<0 nastepnie liczysz delte z pierwotnego rownania wynik (delta) < 0 wychodza ci 2 przedzialy i nastepnie bierzesz z nich czesc wspolna i dla tych m'ów owa funkcja przyjmuje tylko wartosci ujemne

asia: wyszło mi ze 1. m²−4<0. => me(−2,2) 2. delta<0. ==> me(−nieskończoności,−2√2)U(2√2,+nieskończoności) A jaka jest wspólna cześć tego przedziału?