Wykres, wartość bezwzględna, parametr Weronika : Wykorzystując wykres odpowiedniej funkcji ustal liczbę rozwiązań równania w zależności od wartości parametru m: |x²−2|x||=m Moglabym kogos prosic przynajmniej o naswietlenie jak zrobic to zadanie?

Jerzy: Najpierw narysuj wykres: y = x² − 2|x| ( potrafisz ?) potem odbij to co pod osią OD nad oś presuwaj prostą y = m wzdłuż osi OY i sprawdzaj w ilu punktach przecina wykres w zależności od m

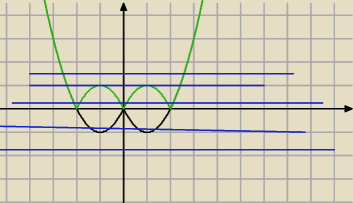
Krzysiek60: jesli Ci tak bardzo na tym zalezy Zauwaz z efunkcja y= x²−2|x| jest parzysta wobec tego rysujemy y= x²−2x do x≥0 i teraz odbijamy ja symetrycznie wzgledem osi OY Teraz to co pod osia OX wedruje nad os i masz y=|x²−2|x|| Tak otrzymany wykres tniesz prosta y=m czarny x²−2|x| zielony |x²−2|x||

Weronika: Rysując pierwszy wykres musze rozpatrzyć dwa przypadki? Dobrze rozumiem? Mam na mysli, ze raz przyjme, ze x≥0 i raz, ze x<0

Jerzy: Tak,możesz rozpatrzyć dwa przypadki,albo wykorzystać parzystość funkcji.

Weronika: No i super, dziekuje Wam bardzo za pomoc!