Min i max funkcji
Krzysiek60: Mozna wykazac ze dla dowolnych liczb a
1,a
2,,,,,,,,,a
n zachodzi nierownosc
| a1+a2+...an | | n | |
| ≥n√a1*a2*...*an≥ |
| |
| n | | 1/(a1)+1/(a2)+....+1/(an) | |
Przy czym rownosci zachodza wtedy i tylko w tedy gdy a
1=a
2=.....=a
n
jest to nierownosc niedzy serdnimi arytmetyczna , geometryczna i harmoniczna
Mam 4 zadania gdzie te nierownosci miedzy srednimi mam wykorzystac do obliczenia najwiekszsej
i najmniejszsej wartosci funkcji.Prosilbym o wytlumaczenie dlaczego takie a nie inne
nierownosci nalezy wykorzystac
Na razie pochodne odpadaja .
Mozna mi tez bedzie pokazac inna metode niz ta . Przy funkcji kwadratowej nie ma problemu
znalezc min czy max
czy to na przedziale czy w calej dziedzinie .
Zadanie nr 1
Wykorzystujac te srednie znajdz najwieksza wartosc funkcji
21 paź 13:02
Adamm:
Nie prawda że dla dowolnych. Dodatnie muszą być
dla x≥0
f(x)=1 wtedy i tylko wtedy gdy x
2=1 ⇒ x=1
teraz, f(−x)=−f(x), więc dla x<0, −1≤f(x)≤0 i f(x)=−1 dla x=−1
21 paź 13:08
Adamm:
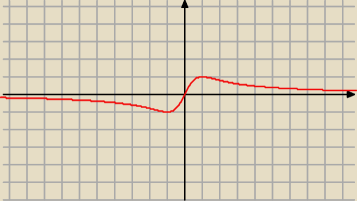
21 paź 13:09
Krzysiek60: czesc
Znowu pominalem dodatnich .
A co ze srednimi ? Jakie i jak wykorzystac ?
21 paź 13:13
Adamm:
Wystarczy am−gm
a1 = x2, a2=1
21 paź 13:34
Krzysiek60: No ok.
| | x2+1 | |
Ale jak wykorzysatm to dostane |
| ≥√x2 to dojde do nierownosci przwdziwej |
| | 2 | |
jak to zapisac w tym zadaniu ?
21 paź 14:41
Krzysiek60: Popi.......e to w ogole jest

21 paź 14:44
Krzysiek60: Dojde do pochodnych i zrobie .
Nastepne moze komus sie przydadza z nierownosci srednich
Zadanie nr 2
Najmniejsza i najwieksza wartosc funkcji
Zadanie nr 3
| | 48 | |
Najmniejsza wartosc funkcji f(x) x3+ |
| x∊R |
| | x | |
Zadanie nr 4
Najwieksza wartosc funkcji f: (0,1)→R i f(x)= x
4−x
6
Zadanie nr 5
Korzystajac z nierownosci Schwarza wyznacz najwieksza wartosc funkcji f(x)=
√x+4
√1−(x/2)
f(x) doprowadzam do f(x)=
√x+2
√2√2−x
i teraz a
1= 1
a
2= 2
√2
b
1=
√x
b
2=
√2−x
Nierownosc Schwarza
|a
1*b
1+a
2*b
2|≤
√a12+a22*
√b12*b22
po podstawieniu i obliczeniu wyszlo mi 3
√2
21 paź 15:59
Omikron:
| | 16 | | 16 | | 16 | |
W zad 3 f(x) = x3 + |
| + |
| + |
| |
| | x | | x | | x | |
Z nierówności między średnimi
| | 16 | | 16 | | 16 | |
| ≥ ({x3* |
| * |
| * |
| )(1/4) |
| 4 | | x | | x | | x | |
Po prawej stronie x się skróci.
21 paź 16:08
Adamm:
@Omikron
możesz tak zrobić dla x≥0
co będzie dla x<0 ?
21 paź 16:45
Omikron:
Pewnie powinienem dopisać, że za dziedzinę uznałem R+. Krzysiek pisał wcześniej, że zapomina
tego dodawać, więc musiało o to chodzić.
21 paź 16:50
Adamm:
Załóżmy że nie zapomniał dodać że R+, i jest R\{0}
jak wtedy byś to zrobił?
21 paź 16:57
Omikron: Pewnie liczyłbym pochodną i ekstremów szukał
21 paź 17:06
Adamm:

f(−x) = −f(x)
jaki z tego jest wniosek?
21 paź 17:23
Omikron:
Nie będzie istniała wartość najmniejsza. Będzie tylko wartość najmniejsza dla jakiegoś x przy
D = R+ i wartość największa dla −x przy D = R−
21 paź 17:33
Krzysiek60: Wracam do zadania z 13 :02 i nr 2 ,3, 4 z 15 :59
Prosilbym o dokladne rozpisanie i wytlumaczenie dlaczego tak ?
25 paź 21:23
25 paź 21:45
Krzysiek60: Dobry wieczor

Do tego zadania mam tak:
| | 1 | | −1 | |
najwieksza wartosc wynosi |
| a najmniejsza |
| |
| | 2√ab | | 2√a*b | |
Wskazowka f jest nieparzysta i dla x>0 f(x)>0 zas dla x<0 f(x)<0
zatem dla pewnego x∊R
+ f moze osiagnac wartosc najwieksza .Zastosuj nierownosc miedzy srednia
arytmertyczna a geometryczna dla liczb ax
2i b gdzie x∊R
+
Nie wiem jak bo znowu dojde do nierownosci prawdziwej jak poprzednio
Dlatego zalezy mi na rozwiazaniu i ewentualnie wytlumaczeniu .
25 paź 21:56
Krzysiek60: | | 4 | |
Do zadania nr 4 mam tylko odp. Najwieksza wartoscia jest |
| |
| | 27 | |
Do zadania nr 3
Najmniejsza wartosc jest 32
Wskazowka zastosuj a
m−g
m .
Do nr 1. Najwieksza wartosc to 1
Wskazowka Wykorzystaj nierownosc miedzy srednia harmoniczna i geometryczna dla liczb x i
25 paź 22:00
Adam:
A jakieś własne pomysły?
25 paź 23:09
Krzysiek60: Adamm wybacz ale takie pisanie nic nie da
napisalem o 14 : 41 ze dochodze do nierownosci prawdziwej a to mi nic nie daje .
25 paź 23:13
jc: x ∊ (0,1)
a=b=x
2/2
c=1−x
2
1/3 ≥
3√(x2/2)(x2/2)(1−x2)
1/27 ≥ (x
2/2)(x
2/2)(1−x
2)
4/27 ≥ x
4−x
6
Równość mamy w przypadku x
2/2=1−x
2, czyli dla x=
√2/3.
25 paź 23:37
Krzysiek60: dzieki jc i dobranoc
Jutro sie nad tym zastanowie po powrocie
26 paź 00:02


 f(−x) = −f(x)
jaki z tego jest wniosek?
f(−x) = −f(x)
jaki z tego jest wniosek?
 Do tego zadania mam tak:
Do tego zadania mam tak: