W okrąg o równaniu wpisano trapez...
matem: W okrąg o równaniu x2 + y2 − 6x − 8y = 0 wpisano trapez tak, że jedna podstawa trapezu jest
jednocześnie średnicą okręgu. Wiedząc, że druga podstawa trapezu zawiera się w prostej o
równaniu x − 2y = 0 oblicz pole trapezu i znajdź równanie jego osi symetrii.
Czy ktoś może pomóc?
20 paź 16:13
Krzysiek60: Skoro trapez ma miec os symetrii to bedzie trapez rownoramienny
20 paź 16:19
Tadeusz:
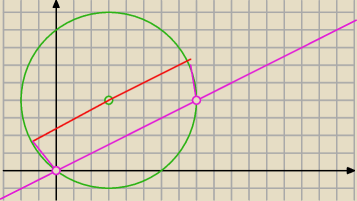
ten okrąg to:
(x−3)
2+(y−4)
2=5
Jedna podstawa to średnica długośc drugiej policzysz po wyznaczeniu punktów przecięcia
prostej i okręgu. Wysokość wyznaczysz jako odległość środka okręgu od prostej.
20 paź 16:25
Tadeusz:
Oś symetri to prosta prostopadła do danej prostej i przechodząca przez S=(3, 4)
20 paź 16:28
matem: dziękuje
20 paź 17:07
Tadeusz:
20 paź 17:08