K Kasia: Wykaz monotonicznosc funkcj

	nn		(n+1)n−1
1)an=		I wychodzi mi tutaj		I nie mam pojęcia co z tym zrobić 🙄
	n!		(n+1)!

Kasia: Tam −1 tez w potedze

Krzysiek60: a_n+1= U{(n+1)ⁿ⁺¹}{(n+1)! (n+1)ⁿ⁺¹= (n+1)ⁿ*(n+1) (n+1)!= n!(n+1) dzielisz teraz U{a_n+1{a_n} powodzenia

Krzysiek60: poprawie

	(n+1)n+1
an+1=
	(n+1)!

jc:

	5		5		5		5
a5=
	1		2		3		4

	6		6		6		6		6
a6=
	1		2		3		4		5

Każdy z ułamków w górnym wierszu jest mniejszy od ułamka leżącego pod spodem, a na dodatek na dole widzimy dodatkowy ułamek większy od 1. Wniosek: a₆ > a₅. W ogólnym przypadku jest podobnie.

jc:

	(n+1)n+1		(n+1)n		nn
an+1 =		=		>		= an
	(n+1)!		n!		n!

Kasia:

	n+1
Dzięki, a pomożecie jeszcze z an=		oraz an={(−1)n}{n}, bo mimo tamtego przykłady
	n2+1

nie mam pojęcia jak to zrobić

Krzysiek60: Nr 1 ) jest troche liczenia ale policzysz tylko tutaj licznik gdyz mianownik bedzie dodatni bo n∊N wiec bedzie >0

	n+1+1		n+2
an+1=		=
	(n+1)2+1		n2+2n+2

	(n+2)(n2+1)−(n+1)(n2+2n+2)
an+1−an=
	(n2+2n+2)(n2+1)

Tak jak napisalem liczysz tylko licznik (badaj jaki jest jego znak potem znak calego wyrazenia Wpisz sobie do wolframa albo licz recznie

Kasia: juz mi wyszlo, ze malejacy, dziekuje Ci bardzo, a Nr 2 ktos wie jak zrobic

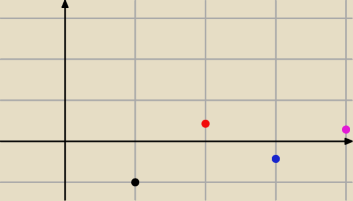
Krzysiek60: Patrz jak sie beda ukladac wyrazy dla n={1,2,3 4 5 itd

	(−1)n
Wiec bedzie rosnacy czy malejacy Nie . wobec tego ciag an=		nie ejst monotoniczny
	n

Kasia: Dziękuje