Inna forma zapisu guntah: Witam, intryguje mnie pewna sprawa, czy mogą obciąć punkty jeśli np. nie skorzystałem z wzoru na sinus podwojonego kąta tam gdzie można było go wykorzystać? Mam odpowiedź identyczną, lecz nie korzystałem z tego więc trochę gorzej to wygląda. Jednak chyba nie powinno być problemu no nie? Wszakże jedno równe jest drugiemu.

PW: Podaj treść zadania, trudno ustosunkować się do takich opowieści. Ocenia się poprawność rozumowania, nie zastosowanie tego czy innego wzoru.

PW: Podaj treść zadania, trudno ustosunkować się do takich opowieści. Ocenia się poprawność rozumowania, nie zastosowanie tego czy innego wzoru.

PW: Znowu "komputer zastanawia się zbyt długo" i nie sygnalizuje wysłania odpowiedzi.

guntah: @PW Oblicz objętość stożka wpisanego w kulę o promieniu R , wiedząc, że kąt rozwarcia stożka ma miarę 2α

PW: Nie będę rozwiązywał. W tym zadaniu nie ma potrzeby stosowania wzoru sin2α=2sinαcosα. Z twierdzenia sinusów

	2r
		=R,
	sin2α

gdzie r oznacza promień podstawy stożka, zatem r mamy wyliczone za pomocą danych R oraz sin(2α). Mając r wyliczymy h (wysokość stożka) jako funkcję kąta α. Podstawić do wzoru na objętość stożka. A to, czy w końcowej postaci coś się skróci, czy nie − ma znaczenie drugorzędne.

	7
Niektórzy np. zostawiają		, inni "skracają" do postaci √7. Nie ma co dyskutować −
	√7

obie wersje sa poprawne: Tego typu wątpliwości masz?

guntah: Między innymi, a ja właśnie słyszałem że trzeba, usuwać niewymierność. Ja to zadanie liczyłem z herona a potem z innego wzoru na pole trójkąta żeby otrzymać r, chyba nawet tak wlasnie tam to rozwiazali i wlasnie nie uzylem wzoru na sinus podwójnego kąta.

guntah:

	n
Chociaż wsm nie wiem czy by sie przyczepili takiego przykladu jak podales
	√n

guntah: @PW sorry chodziło mi o to zadanie: Podstawą ostrosłupa ABCS jest trójkąt ABC , w którym |AB | = 4, |BC | = 6, |CA | = 8 . Wszystkie ściany boczne tworzą z płaszczyzną podstawy kąt 60 stopni . Oblicz objętość ostrosłupa. Dopiero sie skapnąłem że podesłałem ci złe

guntah: ale jednak chyba na jedno wychodzi

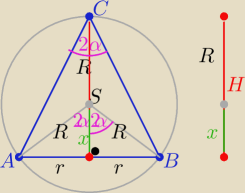
Eta: O licha Heron? ( ale możesz : "jechać z Warszawy do Londynu przez Krym" H=x+R r=R*sin(2α) i x= R*cos(2α) to H= R(1+cos2α)

	1
V=		πR2*H
	3

	1
V=		πR3*sin2α*(1+cos2α) −−− można zostawić taką postać (bo dany jest kąt 2α w treści
	3

====================== żadnych punktów nie stracisz ! lub sprowadzić do postaci zwanej kiedyś logarytmiczną ( jak nie było kalkulatorów i podstawić za : 1+cos2α= 2cos²α i sin2α= 2sinα*cosα

	4
V=		πR3sinα*cos3α
	3

==================

PW: Pięknie, Eta, tyle że "chodziło mu o inne zadanie". Dla przyzwoitości poprawiam, że w moim szkicu rozwiązania zżarłem dwójkę w twierdzeniu sinusów: powinno być

	2r
		= 2R.
	sin(2α)

guntah: Haha, wybaczcie, no tutaj heron nie ma sensu