Oblicz długości podstaw tego trapezu, jeśli jego wysokość jest równa h. genewra: Na trapezie ABCD opisano okrąg o środku w punkcie O i promieniu R. Kąt między dłuższą podstawą AB a promieniem okręgu poprowadzonym do punktu A jest równy 30°. a) R = 10 cm, h = 3 cm b) R = 4 cm, h = 5 cm

genewra: Ktoś pomoże?

Mila: https://brainly.pl/zadanie/5322021

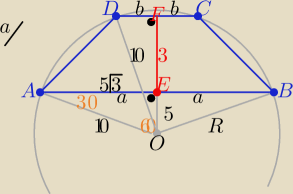
Eta: a) z trójkąta "ekierki" AOE : a= 5√3 to|AB|=10√3 z tw. Pitagorasa w ΔOFD , |OF|=5+3=8 , |OD|=R=10 to b=√100−64= 6 więc ||DC|=2b=12 Odp: |AB|=10√3, |DC|=12 ==================== i po ptokach ( bez brailny ........................................................

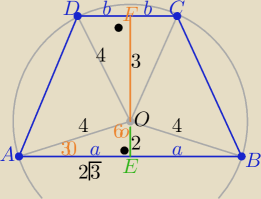
Eta: b) analogicznie jak w a) |AE|=2√3 to |AB|=4√3 z tw. Pitagorasa w ΔOFD b= √16−9=√7 to |DC|=2√7 Odp: |AB|=4√3 , |DC|=2√7 =======================

genewra: Dziękuję