Oblicz pole koła opisanego na prostokącie.
genewra: Oblicz pole koła opisanego na prostokącie o bokach długości 6 cm i 10 cm.
18 paź 21:11
a7: wskazówka, trzeba zrobić rysunek i obliczyć promień, który jest połową przekątnej prostokąta
18 paź 21:19
genewra: Jak obliczyc ten promien?
18 paź 21:23
janek191:
r = 0,5 d
18 paź 21:25
genewra: Skąd mam wiedzieć jaką długość ma przekątna, skoro mam podane tylko długości dwóch boków?
18 paź 21:29
Mila:
Pan Pitagoras Ci powie.
18 paź 21:30
janek191:
Tw. Pitagorasa

d
2 = 6
2 + 10
2 = 136 = 34*4
d = 2
√34
r = 0,5 d =
√34
==============
18 paź 21:31
a7: ok rysuję
18 paź 21:34
a7: a może już jasne?
18 paź 21:35
Mila:
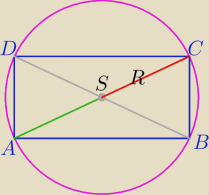
W ΔABC:
|AC|
2=10
2+6
2
|AC|
2=136
|AC|=
√136=
√4*34=2
√34
R=
√34
P
o=π*(
√34)
2=34π
18 paź 21:38
genewra: Do tego punktu już jasne

Teraz mam obliczyć pole?
18 paź 21:43
genewra: A teraz zauwazylam ze pole Milu obliczylas

18 paź 21:44
genewra: To wszystko w tym zadaniu?
18 paź 21:44
Mila:
No przecież nie było jeszcze innego polecenia

18 paź 21:46
genewra: Okej, dziękuję bardzo

18 paź 21:48
Eta:
|AC|=2R to |AC|2=4R2=136 to R2=34
Pk=πR2 = 34π
18 paź 22:41
 d2 = 62 + 102 = 136 = 34*4
d = 2 √34
r = 0,5 d = √34
==============
d2 = 62 + 102 = 136 = 34*4
d = 2 √34
r = 0,5 d = √34
==============
 W ΔABC:
|AC|2=102+62
|AC|2=136
|AC|=√136=√4*34=2√34
R=√34
Po=π*(√34)2=34π
W ΔABC:
|AC|2=102+62
|AC|2=136
|AC|=√136=√4*34=2√34
R=√34
Po=π*(√34)2=34π
 Teraz mam obliczyć pole?
Teraz mam obliczyć pole?


