Ostrosłup prawidłowy trójkątny
Opaw7645: Ostrosłup prawidłowy trójkątny przecięto płaszczyzną przechodzącą przez krawędź podstawy.
Otrzymany przekrój jest nachylony do podstawy pod kątem α.
Oblicz pole P przekroju wiedząc, że krawędź boczna ostrosłupa jest nachylona
do płaszczyzny podstawy pod kątem β, a krawędź podstawy ostrosłupa ma długość a.
18 paź 17:34
a7:
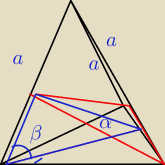
18 paź 17:42
a7: zły rysunek
18 paź 17:53
a7:
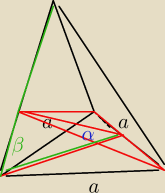
18 paź 17:59
a7: | | a√3 | |
ha − wysokość podstawy ha= |
| |
| | 2 | |
18 paź 18:01
a7:
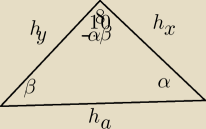
h
a/(sin 180−α−β)==h
x/sinβ
wyliczamy h
x i obliczamy pole przekroju z wzoru na pole trójkąta
P=1/2 a*h
x

18 paź 18:15
18 paź 18:25
Eta:
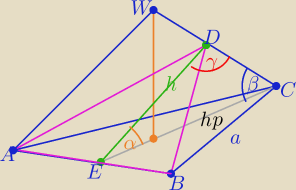
| | h | | hp | |
z tw. sinusów w ΔEDC : |
| = |
| , sinγ= sin(180o−(α+β))= sin(α+β) |
| | sinβ | | sinγ | |
| | 1 | |
P(ABD)= |
| *h = .......... |
| | 2 | |
| | a2√3sinβ | |
P(ABD)= |
| [j2] |
| | 4sin(α+β) | |
=========================
18 paź 18:34
Eta:
| | 1 | |
poprawiam zapis P(ABD)= |
| *a*h |
| | 2 | |
18 paź 18:36
a7: 
18 paź 18:39
Opaw7645: dziękuję bardzo

18 paź 19:23


 ha/(sin 180−α−β)==hx/sinβ
wyliczamy hx i obliczamy pole przekroju z wzoru na pole trójkąta
P=1/2 a*hx
ha/(sin 180−α−β)==hx/sinβ
wyliczamy hx i obliczamy pole przekroju z wzoru na pole trójkąta
P=1/2 a*hx



