Wyznacz monotonicznosc funkcji z def Pi: f(x)= ^2x−1_3x+2 dla x∊D_f więc D_f 3x + 2 ≠0 ⇒ x∊R−{−²₃} niech: x₁<x₂ f(x₂}−f(x₁) = ... = [7(x₂ − x₁) ] / [(3x₂ + 2)(3x₁ + 2 ) ] jak to rozwiazac? :x

PW:

	−2
Iloczyn ten jest dodatni, gdy x1 i x2 są większe niż		:
	3

	2
x1>−		⇒ 3x1>−2 ⇒ 3x1+2>0,
	3

podobnie dla x₂. Ikoczyn ma więc trzy czynniki dodatnie.

	2		2
Gdy x1<−		i x2 <−		, to oba czynniki (3x1+2) i (3x2+2) są ujemne, zatem znowu
	3		3

iloczyn jest dodatni.

	2
Wniosek: f(x) jest rosnąca na przedziale (−∞, −		) i jest rosnąca na przedziale
	3

	2
(−		, ∞).
	3

Nie jest rosnąca w całej dziedzinie, co łatwo pokazać biorąc x₁ z jednego z tych przedziałów, a x₂ − z drugiego.

Pi: Czyli ta funckja nie bedzie monotoniczna ale bedzie rosnaca na tych dwoch przedzialach? A kiedy mozemy powiedziec ze funkcja jest monotoniczna a zarazem rosnaca/malejaca?

Pi: A taki przypadek? f(x) = x²+6x−7 dla x∊R x1<x2 f(x2)−f(x1) = ... = (x2−x1) (x2+3 + x1+3) Jak to teraz dokończyc?

Krzysiek60: A co tutaj dokanczac . Nie jest monotoniczna w calej dziedzinie Co jest wykresem tej funkcji ? Zrob wykres i zobacz

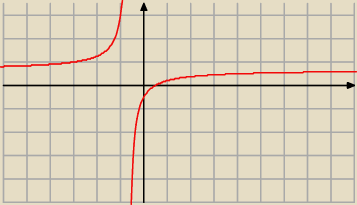
PW: Już odpowiedziałem. Nie jest rosnąca ani malejąca w całej dziedzinie. Jest rosnąca na każdym z

	2		2
przedziałów "w lewo od −		" lub "w prawo od −		".
	3		3

Pi: Krzysiek60 Odczytanie z wykresy bedzie w porzadku jesli w tresci zadania mam wyraźnie " z definicji" ?

PW: Rysunek z 12:08 dotyczy wypowiedzi z 11:48. Dlatego nie należy zadawać dwóch pytań w jednym poście − robi się groch z kapustą.

Pi: PW tak masz racje, dziękuje za pomoc Troszke sie zamieszanie zrobiło. Teraz niestety mnie martwi ta moja wypowiedź z 12:02 i 12:10

Krzysiek60: Moja wypowiedz dotyczyla postu z 12 : 02 Pokaz jak rozpisujesz warunki z postu 12 : 02

Pi: No właśnie problem w tym, że umiem przekształcić f(x2)−f(x1) do takiej postaci jak w poscie 12;02 a następnie nie mam pojęcia co z tym zrobić. Jak to odczytać

Krzysiek60: Zawsze sobie przyjmujesz ze funkcja jest albo rosnaca albo malejaca Przypuscmy ze jest rosnaca wtedy x₁<x₂ to x₁−x₂<0 lub x₂−x₁>0 f(x₁)<f(x₂) to f(x₁)−f(x₂)<0 lub f(x₂)−f(x₁)>0 Ja sobie przyjmuje x₁−x₂<0 f(x₁)−f(x₂) <0

	b
Ta funkcja y= x2+6x−7 dla pw= −−		= −3
	2a

czyli dla x∊−∞−3) jest malejaca i dla x∊(−3,∞) jest rosnaca badaj ja teraz dla x∊(−∞.−3) czyli przyjmujemy ze x₁−x₂<0 f(x₁)−f(x₂)<0 x²₁−6x₁−7−(x²₂+6x₂−7) x₁²+6x₁−7−x₂²−6x₂+7= x₁²−x₂²= (x₁−x₂)(x₁+x₂) x₁−x₂<0 z zalozenia x₁+x₂<0 na tym przedziale bo dodajesz dwie liczby ujemne wiec (x₁−x₂)(x₁+x₂) >0 Wniosek funkcja na tynm przedziale jest malejaca bo zalozylismy ze f(x₁)−f(x₂)<0 Licz na drugim przedziale

Krzysiek60: tzn f(x₁)−f(x₂) = (x₁−x₂)(x₁+x₂) wyjdzie to samo z zalozenia masz x₁−x₂<0 teraz jaki znak ma (x₁+x₂) na tym przedziale x∊(−3,∞) Wniosek i ladna odpowiedz .

Krzysiek60: No i co Pi ? olales .

Pi: Dla x₁,x₂ ∊(−3;+∞) zakładamy f(x₁)−f(x₂) <0 x1² − 6x1 − 7−(−x²+6x2−7) = ... = (x1−x2)(x1+x2) z zalozenia x1−x2< 0 x1+x2 na przedziale moze byc i dodatnie i ujemne?

Pi: Bo w tym przedziale (−3;+∞) są i ujemne i dodatnie? sam juz nie wiem. Nie, nie olałem

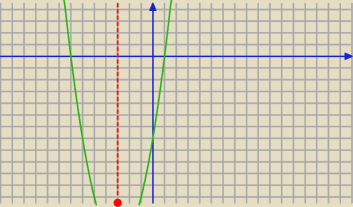
Krzysiek60: dodatnie wiec ? widzisz na wykresie ze od (−3,∞) funkcja ta rosnie czasmi tez dobrze sobie zrobic wykres zeby wiedziec o co chodzi (zwlaszcza ze ten jest prosty do zrobienia

Krzysiek60: Wiesz mi mowiono zeby troche rozstrzelac te wartosci do obliczen np wziac x=−2 i x=100