Dwa proste zadania ze statystyki NieUmiemStatystyki: Zmienna losowa ma rozkład wykładniczy z parametrem λ = 4. Wyznacz dystrybuantę, wartość oczekiwaną oraz wariancję. Niezależne zmienne losowe X i Y mają rozkłady jednostajne na przedziale [1, 3]. Wyznacz rozkład zmiennej losowej Z = X + Y.

Adamm: X ~ Exp(4) https://pl.wikipedia.org/wiki/Rozk%C5%82ad_wyk%C5%82adniczy F(x) = 1−e^−4x, x≥0 EX = 1/4 D²X = 1/16 niezależność jest zbędna X, Y ~ U([1, 3]) https://pl.wikipedia.org/wiki/Rozk%C5%82ad_jednostajny_ci%C4%85g%C5%82y f_Z(x) = f_X * f_Y (x) (tutaj * oznacza splot) f_Z(x) = ∫_−∞^∞ f_X(x−y)f_Y(y) dy = ∫₁³ f_X(x−y) dy = ∫₁³ 1_{[1, 3]}(x−y) dy u=x−y du = −dy f_Z(x) = ∫_x−3^x−1 1_{[1, 3]}(u) du dla x−3≤3≤x−1 ⇔ 4≤x≤6 f_Z(x) = ∫_x−3³ du = 6−x dla x−3≤1≤x−1 ⇔ 2≤x≤4 f_Z(x) = ∫₁^x−1 du = x−2 w przeciwnym wypadku f_Z(x) = 0

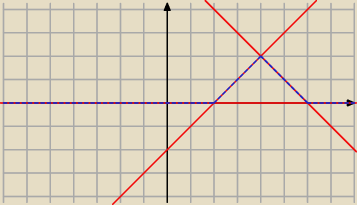
Adamm: rysunek gęstości Z jeśli będziemy dodawać do siebie coraz więcej zmiennych o rozkładzie jednostajnym, nasza gęstość będzie się zachowywać jak wielomian coraz to wyższych stopni (przynajmniej lokalnie na pewnym odcinku)

NieUmiemStatystyki: Super, dziękuję. A skąd bierze się U w 2. zadaniu?

Adamm: U jak uniform distribution