 a) z+z(sprzężone) + i(z−z(sprzężone) = 5+3i
b) √1 √−2 − 3 stopnia
a) z+z(sprzężone) + i(z−z(sprzężone) = 5+3i
b) √1 √−2 − 3 stopnia 

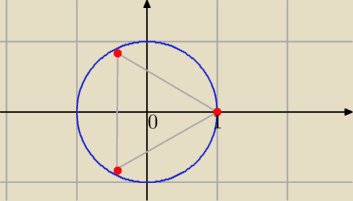 2) Pierwiastki z liczby 1.
Na płaszczyźnie zespolonej pierwiastki n−tego stopnia z jedności są wierzchołkami wielokąta
foremnego o n bokach wpisanego w okrąg jednostkowy,
którego jeden z wierzchołków leży w punkcie 1.
Realizują one podział tego okręgu na n równych części.
z=3√1
2) Pierwiastki z liczby 1.
Na płaszczyźnie zespolonej pierwiastki n−tego stopnia z jedności są wierzchołkami wielokąta
foremnego o n bokach wpisanego w okrąg jednostkowy,
którego jeden z wierzchołków leży w punkcie 1.
Realizują one podział tego okręgu na n równych części.
z=3√1
| 2kπ | 2kπ | |||
zk=cos | +i sin | , gdzie k=0,1,2 | ||
| 3 | 3 |
| 2π | 2π | 1 | √3 | |||||
z1=cos | +i sin | =− | + | i | ||||
| 3 | 3 | 2 | 2 |
| −1+√3*i | ||
z1= | ||
| 2 |
| 4π | 4π | 1 | √3 | |||||
z2=cos | +i sin | =− | − | i | ||||
| 3 | 3 | 2 | 2 |

 Dziękuje za pomoc! <3
Dziękuje za pomoc! <3
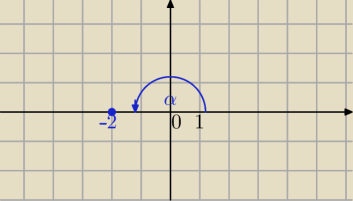 z=3√−2
argument (−2)
α=π
|−2|=2
z=3√−2
argument (−2)
α=π
|−2|=2
| π+2kπ | π+2kπ | |||
zk=3√2*(cos | +i sin | ), k∊{0,1,2} | ||
| 3 | 3 |
| π | π | 1 | √3 | |||||
z0=3√2*(cos | +i sin | )=3√2*( | +i* | ) | ||||
| 3 | 3 | 2 | 2 |
| 1+√3*i | ||
z0=3√2* | ||
| 2 |
| π+2π | π+2π | |||
z1=3√2*(cos | +i sin | )=3√2*(cosπ+i sinπ) | ||
| 3 | 3 |
| π+4π | π+4π | 5π | 5π | |||||
z2=3√2*(cos | +i sin | )=3√2*(cos | +i sin | ) | ||||
| 3 | 3 | 3 | 3 |
| 1 | √3 | |||
z2=3√2*( | − | i) | ||
| 2 | 2 |


| −1+i√3 | −1−i√3 | |||
ω=1 ω1= | i ω2= | |||
| 2 | 2 |
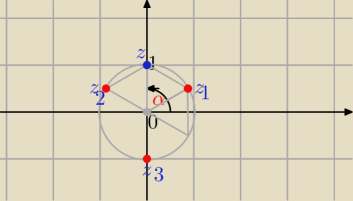 3√i
|i|=1
3√i
|i|=1
| π | ||
arg(i)= | ||
| 2 |
|
| |||||||||||||||
zk=1*(cos | +isin | ), gdzie k∊{0,1,2} | ||||||||||||||
| 3 | 3 |
| π | π | |||
z0=cos | +i sin | |||
| 6 | 6 |
| √3 | 1 | |||
z0= | + | i | ||
| 2 | 2 |
|
| 5π | 5π | |||||||||||||||||
z1=(cos | +isin | )=cos | +i sin | |||||||||||||||||
| 3 | 3 | 6 | 6 |
| √3 | 1 | |||
z1=− | + | i | ||
| 2 | 2 |
|
| |||||||||||||||
z2=(cos | +isin | )= | ||||||||||||||
| 3 | 3 |
| 3π | 3π | |||
=cos | +i sin | |||
| 2 | 2 |