Funkcja różnowartosciowa Mat21: Załóżmy, że x₁, x₂ ∊R, x₁ ≠x₂. f(x) =x ²−2x. Badamy roznowartosciowosc funkcji, f(x₁) − f(x₂)=x₁ ²−2x₁−x₂² + 2x₂ =(x₁−x₂) [(x₁ +x₂) − 2]. Pierwszy nawias jest różny od 0, a drugi w jaki sposób można określić czy jest większy, mniejszy czy różny od zera?

ite: Wynik odejmowania z drugiego nawiasu może równy zero, więc funkcja nie jest różnowartościowa.

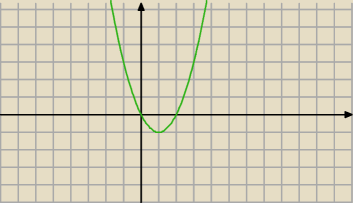
Jerzy: Czy to jest funkcja różnowartościowa ?

aniabb: nie jest różnowartościowa bo dla x₁=2−x₂ będzie f(x₁)−f(x₂) = 0