:( MATH: Wykres funkcji y=|x−2| przecina okrąg o: x² + y² − 4x − 4 = 0 w punktach A i B. a) Oblicz współrzędne punktów A i B b) Wykaż, że trójkąt ABS, gdzie S jest środkiem okręgu o, jest prostokątny c) Oblicz pole figury F=F₁∩F₂, jeśli F₁={(x,y): x∊R ⋀ y∊R ⋀ x² + y² − 4x − 4 ≤ 0}, F₂={(x,y): x∊R ⋀ y∊R ⋀ y ≤ |x−2|}.

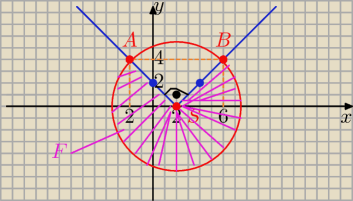
nestor: niebieski wykres ; y= |x−2| czerwony wykres o: ( x −2)²+y²= 8 S( 2,0) r= 2√2 foletowa część to figura F dla x≥2 półprosta y= x −2 wsp. kier. a₁= 1 dla x<2 półprosta: y= −x +2 wsp. kier. a₂= −1 to a₁*a₂=−1 więc te półproste są prostopadłe |< ASB|= 90^o więc trójkąt ASB jest prostokątny i równoramienny dla x≥2 y= x −2 i (x−2)²+y²= 8 −−−−−−− rozwiąż układ równań i wyznacz wspołrzędne A dla x <2 y= −x +2 i (x−2)²+y²=8 −−−−−−−−−− wyznacz współrzędne B A(6,4) B( −2,4)

	3		3		3
pole figury F =		Pkoła =		*πr2 =		*8π= 6π
	4		4		4

Pole F=6π [j²]

mateoxc: Znalazłem błąd: A(0,2) i B(4,2),reszta ok.