monotoniczność x/lnx marcin: czy dobrze liczę? monotoniczność x/lnx pochodna f(x) =x/lnx to f`(x)=(lnx−1)/(lnx)<sup>2</sup> dziedzina (0,1)u(1,+00) rosnąca dla f`(x) lnx−1>0 lnx>1 x c (e,+oo) malejąca lnx−1<0 lnx<1 x c (0, 1)

Blee: A co dla x∊(1;e) Tam już malejąca nie jest

marcin: przepraszam, pomyliłem, oczywiście chodziło o (0, e) a nie (0,1)

Blee: skoro (0,e) to jest źle bo funkcja jest malejąca w (0,1) i w (1;e) dlaczego ... bo x=1 NIE NALEŻY DO DZIEDZINY (masz tam asymptotę)

marcin: czyli powinienem zapisać (0,1)u(1,e) ? muszę to jakoś wyliczać czy powołać się po prostu na dziedzinę?

Blee: W ŻYCIU NIGDY ... przenigdy w monotoniczności nie używa się znaku sumy zbiorów przedziały wypisuje się po przecinku np. funkcja rośnie w przedziale (−5, −4) ; (−4;0) ; (5;8)

Blee: znak sumy oznacza bowiem, że dla (0,1)u(1,e) zachodzi chociażby: f(−0.5) > f(2) co NIE MUSI być (i w przeważającej liczbie przypadków nie będzie) prawdą

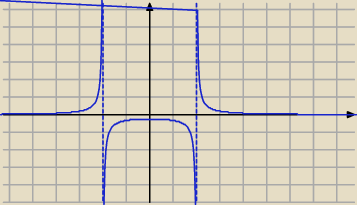
Blee: jak na przykład tutaj

	1
funkcja f(x) =
	x2−4

funkcja ta jest malejąca w przedziale (0,2) oraz w przedziale (2;+∞) ale nie prawdą jest, że f(1) > f(3) ... prawda

marcin: Dziękuję za podpowiedź dobry człowieku