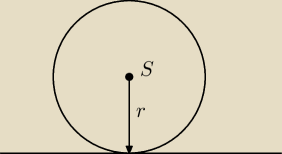
 Skoro ma byc stycny to musi miec jeden punkt wspolny z okregiem a to oznacza ze odleglosc
punktu S od prostej to dlugosc promienia tego okregu
jest na to wzor wiec policz ten promien
Rownanie okregu bedzie takie
(x−5)2+(y−4)2= r2 ( promien ma byc w kwadracie
Skoro ma byc stycny to musi miec jeden punkt wspolny z okregiem a to oznacza ze odleglosc
punktu S od prostej to dlugosc promienia tego okregu
jest na to wzor wiec policz ten promien
Rownanie okregu bedzie takie
(x−5)2+(y−4)2= r2 ( promien ma byc w kwadracie
 To wlasnie napisalem
To wlasnie napisalem

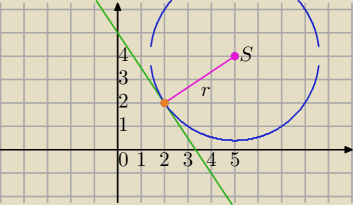 S=(5,4)
k: 3x+2y−10=0
S=(5,4)
k: 3x+2y−10=0
| |3*5+2*4−10| | ||
d(S,k)=r= | ||
| √32+22 |
| 13 | ||
r= | ||
| √13 |
| 13 | ||
(x−5)2+(y−4)2=( | )2⇔ | |
| √13 |