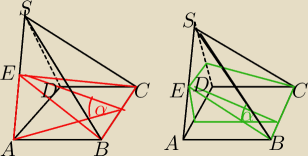
Płaszczyzna w bryle antonio: witam, mam pewną zagwozdkę. Podstawą ostrosłupa ABCDS jest kwadrat ABCD. Trójkąt równoramienny ASD jest prostopadły do podstawy ostrosłyga. narysuj kąt nachylenia płaszczyzny BCE do płaszczyzny podstawy, gdzie E jest środkiem krawędzi SA. Na początku byłem przekonany iż to ma wyglądać tak jak na lewym rysunku, jednak okazało się że ma wyglądać jak na prawym i się zastanawiam dlaczego. To co ja narysowałem byłoby poprawne gdyby chodziło o przekrój tak? Płaszczyzna nie może być trójkątna, o to chodzi?

iteRacj@: Płaszczyzna (nieskończona) została wyznaczona przez trzy punkty B,C,E. Płaszczyzna ma punkty wspólne z wszystkimi 4 krawędziami i ze ścianami bocznymi, bo istnieje również "na zewnątrz" ostrosłupa. To, co narysowałeś, nie jest przekrojem, nie przecina całego ostrosłupa. Nie wiem, czy moje pisanie jest jasne...

iteRacj@: łatwiej pokazać niż opisać https://www.geogebra.org/3d/hpj7vuex

konrad: Jak masz dwie płaszczyzny, które się przecinają, to tworzą one w miejscu przecięcia prostą. Jak teraz poprowadzisz w każdej płaszczyźnie prostą prostopadłą do prostej przecięcia się płaszczyzn, to kąt pomiędzy tymi dwiema prostymi jest kątem nachylenia jednej płaszczyzny do drugiej.

antonio: iteRacj@ dzięki za wyjaśnienie i link do ciekawej strony. Mam tylko jeszcze pytanie, jak nazwać sytuację przedstawioną na pierwszym rysunku? To poprostu kąt nachylenia trójkąta CBE względem podstawy ABCD?

iteRacj@: Na czerwonym rysunku nie jest zaznaczony kąt nachylenia ani trójkąta ΔCBE ani płaszczyzny CBE względem podstawy ABCD. Dlatego że nie leży w płaszczyźnie prostopadłej do krawędzi ostrosłupa. Najlepiej opisał to konrad .

antonio: A dobrze, teraz rozumiem, dzięki iteRacj@, konrad