wiedzac ze tgx = pierwiastek z 2 oblicz sin cos i ctg Rivit: Wiedząc, że tg x = √2 oraz x ∊ (π, ³₂π) Oblicz sin x, cos x, ctg x

Krzysiek60:

	a
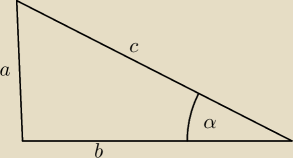
tgα= √2 to z definicji tangensa jest tgα=		stad a= √2 b=1 oblicz c i masz
	b

sinus i cosinus

	1
a cgtα=
	tgα

Pamietaj z ejestes w 3 cwiartce

Rivit: Głupie pytanie, ale czy moge skorzystac ze tg to sin/cos i potem z jedynki trygonometrycznej?

Krzysiek60: Oczywiscie

Krzysiek60: Sprobuj tez zrobic tak

	sinα
Biorac za punkt wyjscia ze tgα=		oraz to ze cosα= √1−sin2α dprowadz do
	cosα

postaci

	tgα
sinα=
	√1+tg2α

======================

	sinα
Biorac za punkt wyjscia tgα=		i poslugujac sie wzorem
	cosα

sinα= √1−cos²α wyprowadz rownosc

	1
cosα=
	√1+tg2α

===================== Majac dany tgα mozesz od razu obliczyc sinα i cos α

Rivit: Faktycznie! Dzięki!

Krzysiek60: na zdrowie

Mila:

	3
tgx=√2 i x ∊ (π,		π)⇔sinx<0 i cosx<0
	2

	1
ctgx=
	√2

sinx
	=√2
cosx

sinx=√2cosx sin²x+cos²x=1⇔(√2 cosx)²+cos^x=1

	1
3cos2x=1 ⇔cos2x=
	3

	1
cosx=−
	√3

	√2
sinx=−
	√3

============

Krzysiek60: Dobry wieczor Milu Skoczylem tamto zadanie .