Przecięcie zbiorów kasia: ∞ ∩ {(x,y) ∊ R² : y²≥nx²} n=1 Rozpisałam to tak: y≥√n x v y≤−√n x Jednak z rysunku niewiele udaje mi się odczytać... wydaje mi się, że iloczynem będzie pkt (0,0), jednak nie jestem pewna czy w ogóle to jest dobry sposób.

iteRacj@: https://www.geogebra.org/graphing/evd9fukf bez rozpisywania, łatwiej będzie zobaczyć część wspólną, uruchom suwak

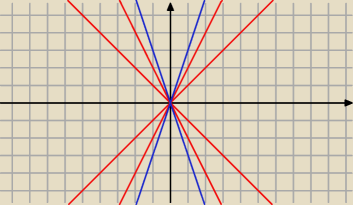
Adamm: zbiory "sciągają" się do prostej x=0

Adamm: a biorąc dowolny punkt z tego zbioru y²/n≥x² dla każdego n, więc przechodząc do granicy, 0≥x² ⇒ x=0 czyli, jeśli punkt (x, y) należy do tego zbioru, to x=0, ale na odwrót, każdy taki punkt należy do tego zbioru

kasia: Hm, ale biorąc pod uwagę, że mamy tam nierówności, to ostatecznie co będzie iloczynem? Coś więcej niż punkt (0,0)?

Adamm: (0, y), y∊R

iteRacj@: 9:56 iloczynem będzie prosta x=0, ona należy do każdego ze zbiorów

kasia: Już to widzę. Mój rysunek był nieczytelny. Dziękuję i życzę miłej soboty.